Les QCM interactifs sont accessibles � partir de la page d�accueil
du coaching virtuel � acc�s gratuit dilingco.com
Page 1.
Quelques d�finitions

S�lectionner
les deux affirmations exactes :
1-
Bouteille en plastique ferm�e : exemple de syst�me thermodynamique isol�
2- Une
variable extensive est proportionnelle � la taille du syst�me
3- Les variables
d��tat ont des valeurs qui d�pendent du chemin suivi pour atteindre l��tat
consid�r�
4- La
chaleur Q est une variable d��tat
5- Les
variables d��tat sont ind�pendantes les unes des autres (Pas d��quation d��tat
entre elles)
6- [A].
Fonction d��tat : ne d�pend que de l��tat syst�me consid�r�. Entre 2
�tats, ne d�pend pas du chemin suivi
7- Les
transformations ne peuvent pas �tre d�finies en prenant une variable d��tat
constante
Les
affirmations 2 et 6 sont exactes.
�
Affirmation
1
Non.
Bouteille
en plastique ferm�e : Syst�me thermodynamique
ferm�.
Un
syst�me thermodynamique ferm� peut �changer :
- un
travail avec le milieu ext�rieur (la paroi est d�formable),
- de la
chaleur avec le milieu ext�rieur.
Un syst�me ferm� ne peut pas d��change de mati�re avec le milieu
ext�rieur.
Exemple
de syst�me isol� (aucun �change avec le milieu
ext�rieur) :
Bouteille
thermos ferm�e id�ale ; pas d��change de mati�re, pas d��change d��nergie
sous forme de chaleur, d��lectricit�, de travail (parois ind�formables) etc.
�
Affirmation
2
Oui.
Une variable extensive (d�pend de l�extension du syst�me) est proportionnelle � la taille du syst�me.
Exemples : nombre de moles, masse, volume, quantit� de chaleur Q
Les
variables extensives peuvent s�additionner.
Exemple :
Volume total = volume1 + volume2.
Une variable intensive ne d�pend pas de l�extension
du syst�me, de la quantit� de mati�re.
Exemples :
Temp�rature
T.
Unit� :
degr� kelvin. O�k= -273,15 �C
Pression
P. (Force par
unit� de surface).
Unit� :
pascal (1 N/M2) ou le bar 1 bar = 100 000 Pa
(Ancienne
unit� : 1 atmosph�re = 1,01325.105 Pa)
Masse
volumique (p ou�), masse par unit� de volume,
Concentration
c, concentration
massique, concentration molaire)
Fraction
molaire x,
proportion d�un composant dans un m�lange.
xi
= ni / ntotal
Affirmation
3
Non.
Une variable d��tat caract�rise un �tat du syst�me.
Elle ne d�pend pas du chemin suivi pour atteindre l��tat
Principales
grandeurs d��tat :
- Temp�rature T (mesure de l�agitation �lectronique � un instant
donn�)
- Pression P
- Volume V, m3
- Energie interne U, J/kg
- Enthalpie H, J/kg
- Entropie S, J/k (joule par kelvin)
Affirmation
4
Non.
La chaleur Q :
- transfert d�sordonn� d��nergie thermique entre 2 syst�mes � temp�ratures
diff�rentes,
- n�est pas
une variable d��tat (d�pend du chemin choisi),
-
unit� : (comme celle des autres �nergies) = joule.
Autre
grandeur thermodynamique qui n�est pas une variable d��tat : le travail W, �nergie m�canique d�une force qui se d�place. Unit� : joule.
Affirmations
5
Non.
Les diff�rentes variables d��tat ne sont pas ind�pendantes entre elles.
Des
� fonctions d��tat � ou � �quations
d��tat � font ressortir les liens entre les variables d��tat.
Exemple :
�quation des gaz parfaits.
(Gaz
parfaits : les mol�cules sont suffisamment �loign�es pour en n�gliger les
interactions).
�
Affirmation
6
Oui.
[A]. Fonction d��tat :
- ne d�pend que de l��tat syst�me consid�r�,
- si la
fonction est �tablie entre 2 �tats, ne d�pend pas
du chemin suivi.
La Loi
d�Avogadro est une �quation d��tat :
Des volumes �gaux de gaz parfaits diff�rents, aux m�mes conditions
de temp�rature et de pression, contiennent le m�me nombre de mol�cules.
Le nombre
de moles :
- est
proportionnel au volume consid�r�, proportionnel � la pression,
-
inversement proportionnel � la temp�rature.
Note :
Gaz
parfaits : les
mol�cules sont suffisamment �loign�es pour en n�gliger les interactions.
Exemples :
O2, N2 de l�atmosph�re.
R :
constante des gaz parfaits = NA. KB = 8,3144621 J⋅K-1⋅mol-1
NA :
nombre d�Avogadro = 6,022 141 29(27)�1023 mol−1.
KB :
Constante de Boltzmann
Affirmation
7
Si.
Tr�s
souvent les transformations sont d�finies avec une variable d��tat constante.
Transformation isotherme : �
temp�rature constante
Isobare : � pression constante,
Isochore :
� volume constant,
Isoenthalpique : � enthalpie constante,
Isoentropique : � entropie constante.
Adiabatique : pas d��change de chaleur avec le milieu ext�rieur.
Page 2.
Principes de la
thermodynamique

S�lectionner
les deux affirmations exactes :
1- [A]. 1
et 2 en �quilibre thermique, 2 et 3 en �quilibre thermique = Les trois syst�mes
sont en �quilibre thermique entre eux
2- [B]. Q2=Q1. L��nergie se conserve mais peut prendre des formes diff�rentes
3-
L��volution d�une r�action dans un syst�me isol� n�est jamais pr�dictible,
jamais irr�versible, et ne d�pend pas de consid�rations thermodynamiques
4- La thermodynamique s�int�resse aux processus de r�actions chimiques, � la
vitesse de r�action, aux fonctions et dur�es d��volutions
5- [C]. L��nergie
d�un syst�me ferm� baisse : l��nergie du syst�me isol� qui le contient
baisse aussi
Les
affirmations 1 et 2 sont exactes.
Voir Physique, thermodynamique, Principes
Affirmation
1
Oui.
Principe
0 de la thermodynamique : Equilibre thermique.
Deux syst�mes en �quilibre thermique avec un troisi�me sont aussi
en �quilibre thermique entre eux.
Affirmation
2
Oui
Principe
1 : L��nergie
se conserve.
L��nergie peut prendre des formes diff�rentes : agitation thermique
mol�culaire, travail m�canique, etc.
Pour un syst�me isol� :
Somme des
diff�rentes formes d��nergies en Q2 = somme des formes d��nergies en Q1.
Affirmation
3
Si.
Deuxi�me principe : principe d��volution & d�entropie.
L��nergie
passe irr�versiblement de formes concentr�es
et potentielles, � des formes diffuses, d�sordonn�es, et cin�tiques.
Le
deuxi�me principe introduit la notion d�entropie.
L�entropie S est la mesure du d�sordre : Dans un
syst�me isol�, l�entropie (le d�sordre) augmente
de mani�re irr�versible.
En
thermodynamique classique, l�unit� de l�entropie, quantit� de chaleur �chang�e
par un syst�me, � temp�rature T constante, est le joule
par kelvin.
Affirmation
5
Non.
Principe 1 : L��nergie se conserve.
Une perte en �nergie du syst�me interne va entra�ner une augmentation d��nergie
dans son milieu ext�rieur pour rester conforme, globalement, au deuxi�me
principe de la thermodynamique.
Q interne baisse => Q environnement augmente
(L��nergie
diffus�e augmente l��nergie environnementale)
Q total =
Q interne + Q environnement => augmente ou reste constante
- Reste
constante si le syst�me global est en �quilibre ou �id�alement� proche de
l��quilibre,
- Q ne
peut pas diminuer : principe de la conservation de l��nergie d�un syst�me
isol�.
Note :
Syst�me
ferm� = permissible � l��nergie.
Principes
de la thermodynamique
Quatre principes r�gissent la thermodynamique.
Le premier et le deuxi�me principe sont les plus
importants.
- Principe 0 : �quilibre thermique
- Premier principe : principe de conservation
de l��nergie.
L��nergie d�un syst�me isol� est constante ; Les formes de l��nergie peuvent varier (l��nergie
se transforme)
- Deuxi�me principe : principe d��volution de l��nergie & entropie.
L��nergie passe irr�versiblement de formes : Concentr�es et
potentielles, �
des formes, diffuses, d�sordonn�es, et cin�tiques.
Le
deuxi�me principe introduit la notion � d�entropie �.
L�entropie
est la mesure du d�sordre d�un
syst�me.
Le
deuxi�me principe permet de pr�voir le sens d�une
r�action chimique et� l��quilibre
chimique d�une r�action.
- Troisi�me principe : un syst�me qui descend vers son �tat quantique fondamental
voit sa temp�rature s�approcher du z�ro absolu
(O�
Kelvin= - 273,15� C)
Page 3.
Entropie. Syst�me isol�
S�lectionner les deux affirmations exactes :
1- [A]. Un
syst�me isol� atteint un �tat d'�quilibre lorsque son entropie S devient minimale
2-
Transformation irr�versible : L�entropie globale (entropie interne du
syst�me ferm� + entropie milieu ext�rieur) augmente
3- Dans
un syst�me isol� l�entropie peut d�cro�tre
4- Un corps pur parfait, � la temp�rature absolue 0 Kelvin, est parfaitement
ordonn�. Son entropie S est nulle
5- Les d�finitions de l�entropie S en thermodynamique classique,
S=Q/T, et en thermodynamique statistique ([C]. Formule de Boltzmann), sont
contradictoires
6- L�entropie n�est pas une variable d��tat
Les affirmations 2 et 4 sont exactes.
Voir Physique, thermodynamique, Entropie
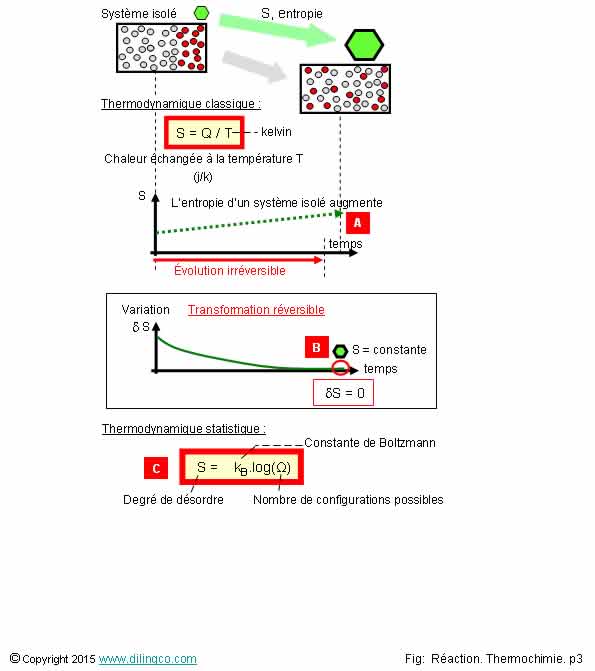
Affirmation 1
Non.
[A] :
Un syst�me atteint
un �tat d'�quilibre lorsque son entropie S� devient maximale.
L�entropie S d�un syst�me isol� ne peut :�������
- qu�augmenter vers une valeur maximale, ou
- rester constante, autour de la valeur S maximale, lorsque un
�quilibre est atteint (On dit alors que la transformation est r�versible).
On peut noter :
L�entropie refl�te la capacit� d�un syst�me � �voluer.
Plus l�entropie est faible, plus le syst�me peut �voluer.
Plus le syst�me �volue, moins il est capable d��voluer.
Affirmation
2
Oui.
[A] : Transformation irr�versible : il y a cr�ation
globale d�entropie.
*D Sglobal = *D Ssyst + *D Sext >0
[B] : Transformation r�versible : la cr�ation d�entropie
est nulle.
Dans le cas d�une �volution id�ale r�versible, on assume qu�il n�y
a pas eu d��mission de chaleur, pas de pertes li�es aux frottements.
Quantit� de chaleur dissip�e Q = 0 donc la variation d�entropie S =
0
Affirmation
3
Non.
Syst�me isol� :
- pas
d��change avec le milieu ext�rieur,
-
l��nergie y est constante mais peut prendre des formes diff�rentes,
- Syst�me isol� : l�entropie ne peut pas d�cro�tre.
Elle ne peut qu�augmenter ou rester constante si l��tat final est atteint.
Note :
Un syst�me non isol� peut avoir une variation d�entropie n�gative s�il produit une
variation d�entropie positive sur son environnement.
Affirmation 4
Oui.
S = 0 � 0� K
Principe
de Nernst : L�entropie d�un cristal parfait � 0 kelvin est nulle.
Affirmation
5
Non.
Plusieurs interpr�tations de l�entropie sont possibles.
Les d�finitions de Clausius (S=Q/T) et de Boltzmann r�sultent de
consid�ration du syst�me � des points de vues microscopique ou macroscopique du
syst�me mais ne sont pas contradictoires.
Thermodynamique classique
S = entropie = Q/T
Q : quantit� de chaleur �chang�e par un syst�me, consid�r� dans son
ensemble (au niveau macroscopique), � la temp�rature T.
Unit� : J/K, Joule par Kelvin
Thermodynamique statistique
L�entropie est la mesure du d�sordre d�un syst�me au
niveau microscopique.
Plus l�entropie est grande :
- moins ses �l�ments sont ordonn�s, li�s entre eux,
- moins les �l�ments d�sordonn�s peuvent fournir de travail
(Ils gaspillent plus d��nergie pour fournir le travail).
S = kB.log(Ω)
kB est la constante de Boltzmann,
٠est le nombre d��tats
microscopiques dans le syst�me consid�r�.
Ω d�finit la complexit� du syst�me.
Plus le syst�me se
d�sorganise au niveau microscopique, plus le nombre d��tats ٠est important (gigantesque !),
plus l�entropie est grande.
Le nombre Ω ne peut pas �tre d�fini pour la plupart des
syst�mes : l�entropie S ne peut pas ce calculer.
La thermodynamique statique s�applique �
l�imagerie m�dicale par exemple.
Autres d�finitions de l�entropie
Informatique : entropie de Shannon,
Math�matique : entropie topologique, entropie m�trique.
Affirmation 6
Si.
L�entropie est une variable d��tat thermodynamique calculable dans
l�absolue.
(Les autres ne peuvent �tre d�finie que par leurs variations)
Unit� de mesure : j/k, joule par kelvin, en thermodynamique
classique.
Page 4
Enthalpie

S�lectionner
les deux affirmations exactes :
1- Pression
et volume sont des grandeurs intensives
2- La
variation d�enthalpie au cours d�une r�action ne peut pas �tre mesur�e
3- La
variation d�enthalpie lors d�une r�action ne d�pend pas des conditions
ext�rieures
4- Lors
d�une r�action, une diminution de l��nergie du syst�me = r�action exothermique
5- Variation
d�enthalpie � pression constante = chaleur �chang�e => premier principe de
la thermodynamique
6- Il
faut apporter de la chaleur pour qu�une r�action exothermique (diminution de
l�enthalpie) se fasse
Les affirmations
4 et 5 sont exactes.
Voir Physique, thermodynamique, Enthalpie
Affirmation
1
Non
pV d�pend du volume occup� par le
syst�me, c�est une grandeur extensive.
pV
repr�sente le travail que le syst�me doit fournir contre la pression ext�rieure
pour garder son volume.
Affirmation
2
Si.
La variation d�enthalpie (zone entour�e en rouge de la figure) correspond aux
variations de chaleur Q fournie, ou re�ue,
lors d�une r�action.
Mesurer
la quantit� de chaleur �chang�e lors de la r�action revient � mesurer
l�enthalpie.
Affirmation
3
Si.
*DH
d�pend des conditions ext�rieures, des variations de l��nergie environnementale ;
variations de pression ou de temp�rature, par exemples.
Affirmation
4
Oui.
Exothermique : La r�action fournie de la chaleur.
Endothermique : La r�action re�oit de la chaleur.
Athermique
: pas d��change de chaleur
Isochore :
� volume constant.
Isobare :
� pression constante.
Isotherme : � temp�rature constante.
Affirmation
5
Oui.
*DH = Qp
Variation d�enthalpie = chaleur �chang�e (� pression constante)
Premier principe de la thermodynamique : L��nergie se
conserve.
Affirmation
6
Non.
Il faut
apporter de la chaleur pour qu�une r�action endothermique, qui consomme de
l��nergie (variation d�enthalpie positive) se fasse.
Note :
Ceci
d�montre une des utilit�s de la thermodynamique : pouvoir conna�tre, calculer l�enthalpie d�une r�action,
permet de savoir s�il faut chauffer ou non pour qu�une r�action
chimique se fasse.
A se
rappeler
Enthalpie, du grec � chaleur interne � : chaleur (�nergie)
interne + travail de maintient de volume. H = U + pV.
U :
�nergie interne emmagasin�e par le syst�me.
pV : travail pour maintenir le volume occup� par le syst�me.
� pv constant, variation d�enthalpie =
chaleur �chang�e.
L�enthalpie
= �nergie = dimension d�une �nergie.
Unit� : joule
Note :
La connaissance de l�enthalpie (li�e � la chaleur), permet,
par exemples, de choisir le gaz le mieux appropri� pour chauffer un m�lange,
chauffer ou refroidir pour augmenter le rendement d�une r�action chimique, etc.
Page 5.
Enthalpie libre G

S�lectionner les deux affirmations exactes :
1- Pour une r�action [r�actifs ->produits], la variation
d'enthalpie libre est positive
2- Enthalpie libre G : partie de
l�enthalpie utilisable pour produire une transformation chimique ou �lectrique
3- L�enthalpie libre G= H � TS n�est pas li�e au deuxi�me principe de
la thermodynamique (�volution et entropie)
4- L�enthalpie libre G n�est ni une fonction d��tat ni une
variable extensive
5- Syst�me riche en �nergie utilisable = enthalpie libre G de
d�part �lev�e
Les affirmations
2 et 5 sont exactes.
Voir Physique, thermodynamique, Enthalpie libre G
Affirmation 1
Non.
R�action R�actifs -> Produits : variation d'enthalpie libre G diminue
(*DG < 0).
Le signe de l�enthalpie libre permet de pr�voir le sens d�une
r�action.
(Voir pages suivantes)
Affirmation 2
Oui.
Enthalpie libre G : partie de l�enthalpie utilisable pour
produire une r�action chimique, �lectrique, ou un travail.
G : l�enthalpie libre G :
- introduite par Willard Gibbs,
- aussi appel� � �nergie de Gibbs �.
Affirmation 3
Si.
L�enthalpie libre G= H � TS est li�e au 2�me principe de la
thermodynamique par sa variable S, entropie.
2�me principe de la thermodynamique : �volution et
entropie.
Affirmation 4
Si.
La figure montre que l�enthalpie libre est li�e � un �tat du
syst�me.
C�est aussi une grandeur extensible, par sa composante H li�e au
volume.
Enthalpie H = U + pV
Enthalpie libre
L�enthalpie
libre G, est aussi appel�e � �nergie libre de Gibbs �
G : Willard Gibbs.
G = H � TS
H :
enthalpie
T : temp�rature
en degr�s absolus dans l��chelle Kelvin
S : entropie
L�enthalpie libre peut �tre
interpr�t�e comme la partie de l�enthalpie utilisable pour produire une transformation chimique ou �lectrique
(� temp�rature et � pression constante).
Variation
d�enthalpie libre
Le syst�me �volue vers son �tat de plus faible �nergie.
Le signe
de variation de l�enthalpie libre d�termine le sens de la r�action chimique.
R�actions � r�actifs vers produits � :
*D GT,p(sys) = *D H sys � T *D Ssys < 0�
R�actions � produits vers r�actifs � :
*D G T,p(sys) = *D H sys � T *D Ssys > 0�
R�action � l��quilibre :
*D G T,p(sys) = 0 = La r�action s�arr�te.
Page 6.
Enthalpies.
Formation & r�action
S�lectionner l�affirmation exacte :
1- Les
enthalpies standard de formation des r�actifs et produits ne permettent pas de calculer
l�enthalpie standard d�une r�action
2- Les enthalpies standard de formation et de r�action sont pour T=273,15k (0�C) et P=1 atm
3- [B] : Tous les compos�s chimiques ont la m�me enthalpie standard de
formation
4- [A]. L�enthalpie standard de r�action permet de dire si la r�action est
exothermique, endothermique, ou adiabatique
L�affirmation 4 est exacte.
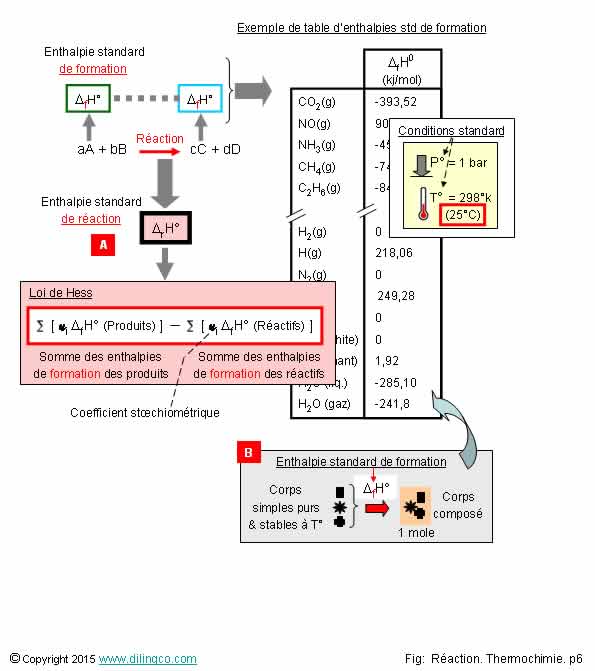
Affirmation
1
Si.
Le calcul de l�enthalpie standard d�une r�action est possible :
*D rH� = Somme des enthalpie de formation des produits � Somme des enthalpies
de formation des r�actifs.
Notes :
- Les coefficients stoechiom�triques entrent dans la formule.
- f = enthalpie de formation,
- r = enthalpie de la r�action,
- � = conditions standard.
Les enthalpies standard de formation des corps compos�s :
- sont d�finies dans des tables,
- peuvent �tre mesur�es exp�rimentalement.
Affirmation 3
Non.
[B]. L�enthalpie standard de formation, chaleur �chang�e lors de la r�action,
d�pend du compos� chimique obtenu.
L�enthalpie
standard de formation :
- not�e *D Hf�,
- variation
d�enthalpie lors de la formation du compos� � partir des corps simples purs,
- dans les conditions de l��tat standard
(p�= 1 bar = 105 Pa. T� = 298k (25�C),
- les corps simples purs doivent �tre dans un �tat stable (gaz ou liquide ou
solide) � l��tat standard,
- des
tables donnent des valeurs de l�enthalpie standard de formation pour les compos�s chimiques
principaux,
- les valeurs
peuvent aussi �tre mesur�es exp�rimentalement en r�alisant la r�action de
composition dans un calorim�tre et en mesurant la chaleur �chang�e.
Affirmation
4
Oui.
[A].
*D H = Qp
Variation d�enthalpie = chaleur �chang�e � pression constante.
Voir page pr�c�dente � Enthalpie �
La variation d�enthalpie standard de r�action permet de dire si la
r�action est :
- exothermique, *D rH < 0, il y a
perte de chaleur lors de la formation du compos� chimique,
- endothermique, *D rH > 0, la
r�action doit recevoir de la chaleur pour se faire,
- adiabatique, *D rH = 0,� pas d��change de
chaleur lors de la r�action.
Page
7.
Enthalpies de formation.
Mesures
S�lectionner
l�affirmation exacte :
1- L�enthalpie de formation des corps compos�s ne peut pas �tre
d�termin�e exp�rimentalement
2- Pas de relation entre la chaleur �chang�e et la variation de
temp�rature
3- L'enthalpie de formation des corps simples (H2, O2, N2, etc),
est par d�finition nulle
4- Pouvoir calorifique = capacit� calorifique
L�affirmation 3 est exacte.
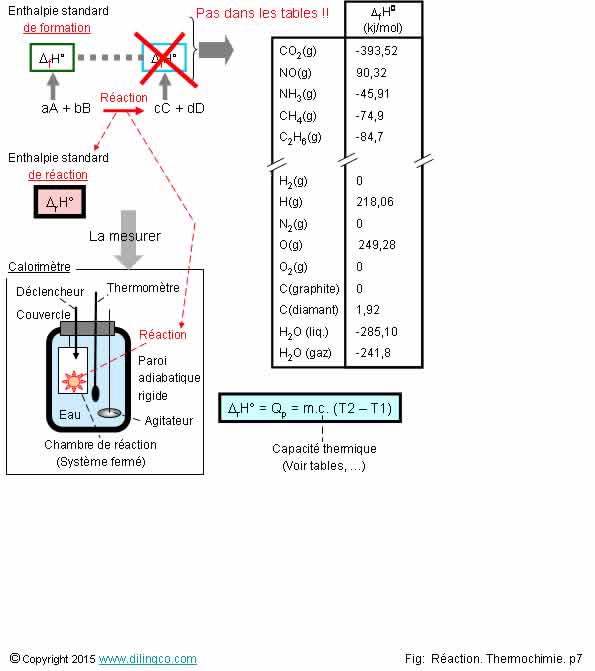
Affirmation 1
Si.
Les enthalpies de formation peuvent �tre mesur�es en r�alisant la
r�action dans un calorim�tre.
D�terminer la variation d�enthalpie revient � mesurer la variation
de temp�rature, puis � d�terminer la chaleur �chang�e lors de la r�action de
constitution du compos� chimique.
Notes :
- Calorim�tre : syst�me isol� destin� � mesurer les �changes de chaleur.
La mesure des variations de temp�rature permet de d�terminer
l��change de chaleur et la variation d�enthalpie.
- Q = m.c. (T2 � T1)
- *D H
= Qp
Variation d�enthalpie = chaleur �chang�e � pression constante.
Voir page pr�c�dente � Enthalpie �
Affirmation 2
Si.
Relation entre chaleur �chang�e et la variation de
temp�rature :
Q = m.c. (T2 � T1)
Q :
quantit� de chaleur en joules
m : masse en kg
c : capacit� calorifique
T : temp�rature en kelvin
Note :
- La capacit� calorifique (ou capacit� thermique) qualit� d�un corps �
absorber/restituer de la chaleur par �change thermique lors d�une variation de
temp�rature.
- on d�finit des capacit�s thermiques massiques cm, (j/kg/k),
volumiques cv (j/m2/k), cm molaires (j/m/k).
Affirmation 3
Oui.
L'enthalpie de formation des corps simples (H2, O2, N2, etc), est
par d�finition nulle : le corps simple pur n�a pas besoin d�une r�action de
formation pour se former, pour se former � partir de lui-m�me.
Affirmation 4
Non.
Pouvoir calorifique :
(ou chaleur de combustion)
- notation : *D cH�,
- unit�s : kilojoule par kilogramme, kilojoule par mole, par
litre
- enthalpie de r�action lors d�une combustion
Exemple : d�un hydrocarbure avec le dioxyg�ne.
Essence : 35 475 kj/L
Capacit� calorifique :
(ou capacit� thermique) qualit� d�un corps � absorber/restituer de la
chaleur
par �change thermique lors d�une variation de temp�rature.
Q = m.c. (T2 � T1)
Unit� :
joule par kelvin.
Page
8.
Table & calcul
S�lectionner
l�affirmation exacte :
1- [A]. Enthalpie molaire standard de r�action
2- [B]. Enthalpie de formation du graphite (carbone corps simple pur
le plus stable aux conditions standard) : 1,92 kj/mole
3- [B]. La formation du diamant � partir du graphite n�cessite de
la chaleur (1,92 kj/mole)
4- [C]. + 103,88
L�affirmation 3 est exacte.
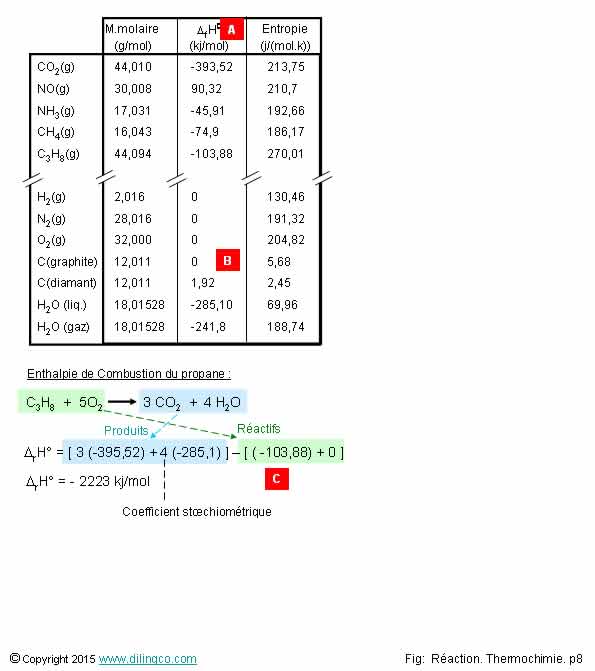
Affirmation 1
Non. [A]. Enthalpie molaire standard de formation des compos�s
chimiques de la premi�re colonne.
(Le � f � de *D fH0 signifie � formation �)
Notes :
La table pr�sent�e est une table simplifi�e.
Des tables d�enthalpies plus compl�tes se trouvent sur
Internet.
L�enthalpie de formation d�un compos� peut toujours se d�terminer
exp�rimentalement� (Voir calorim�tre page pr�c�dente).
Affirmation 2
Non.
[B]. Enthalpie de formation du graphite : 0 kj/mole.
Le graphite, carbone pur simple stable aux conditions standards (1pa,
25�C) n�a pas � se � former � en lui-m�me (C -> C).
Affirmation 3
[B].
Oui. La formation du diamant � partir du graphite n�cessite de la
chaleur.
Enthalpie de formation : 1,92 kj/mole.
Le
diamant n�est pas le carbone le plus stable aux conditions standard.
C(s) graphite -> C(s) diamant�� *D H0 =
1,9 kj/mole
Le carbone est allotropique : il a plusieurs formes solides.
Affirmation 4
Non.
[C]. *D fH0 du propane = - 103,88 (- = r�action
exothermique).
Loi de Hess = Somme des enthalpies de formation des produits � somme des
enthalpies de formation des r�actifs
Attention :
Respecter les signes dans les sommes et ne pas oublier les coefficients
stoechiom�triques.
�
Page 9.
Enthalpie de r�action. T
quelconque
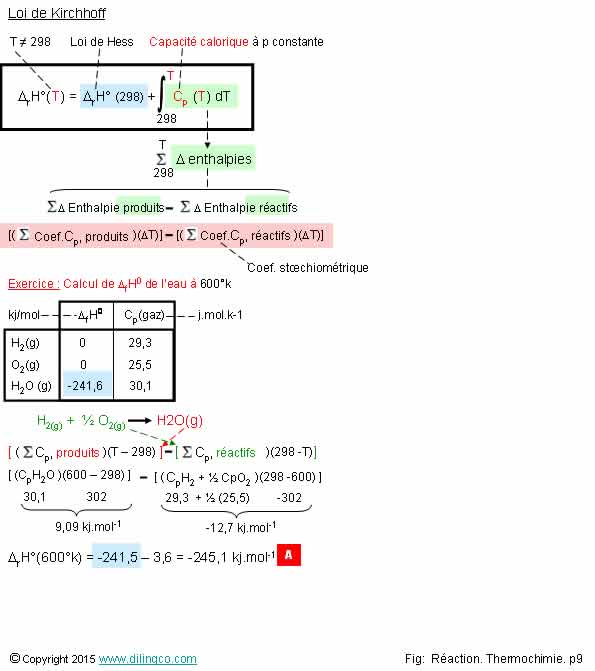
S�lectionner l�affirmation exacte :
1- Conna�tre l�enthalpie standard de r�action et les capacit�s
calorifiques ne permet pas de calculer l�enthalpie de r�action � T quelconque
2- L�enthalpie de la r�action de l�eau � 600�k est identique �
celle � 298�k
3- � pression constante : Enthalpie de r�action = chaleur
�chang�e
4- [A]. Il faut chauffer pour que la r�action se fasse
L�affirmation 3 est exacte.
Affirmation 1
Si.
Voir [A] loi de Kirchhoff.
Enthalpie de r�action � temp�rature T =
Enthalpie standard de r�action + enthalpie de T� � T
(A condition qu�il n�y ai pas de changement d��tat entre les 2
temp�ratures)
Enthalpie de T� � T =
Coeff. Stoechiom�trique x capacit� calorique x DT
Capacit� calorifique :
(ou capacit� thermique) qualit� d�un corps � absorber/restituer de la
chaleur
par �change thermique lors d�une variation de temp�rature.
Q = m.c. (T2 � T1)
Unit� :
joule par kelvin.
Affirmation 2
Non.
L�enthalpie
de r�action d�pend :
- de la temp�rature de la r�action,
- de la phase (gaz, liquide, solide) o� sont les composants.
L�enthalpie de la r�action de l�eau � 600�k = -245,1 kj.mol-1
L�enthalpie de la r�action de l�eau � 298�k = -241,6 kj.mol-1
Affirmation3
Oui.
� pression constante : *D H = Qp
Enthalpie de r�action = chaleur �chang�e
Affirmation 4
Non.
[A]. Perte de chaleur, la r�action est exothermique.
Page 10.
Changement d��tats
La figure pr�sente l��volution de l�entropie pour un corps pur
allotropique (Ici, l�eau pure).

S�lectionner l�affirmation exacte :
1- Pas de lien entre l�entropie, la chaleur, la temp�rature
2- Changement d��tat : la chaleur est enti�rement utilis�e
pour modifier les liaisons mol�culaires (pas de variation de temp�rature)
3- Les capacit�s caloriques de la glace, de l�eau, de la vapeur
d�eau, ont les m�mes valeurs
4- [A]. Variation d�entropie entre Tf et T2 : L�int�grale de dT/T
est Log d�cimal de T2/Tf
L�affirmation 2 est exacte.
Affirmation 1
Si.
T. Temp�rature : variable d��tat. Mesure de l�agitation
�lectronique.
Unit� : � kelvin.
Q.
Chaleur :
transfert d��nergie entre 2 syst�mes � temp�ratures diff�rentes. Se mesure en
joules.
En dehors des changements d��tats : l��nergie re�ue fait
cro�tre l�agitation �lectronique et donc la temp�rature.
S. Entropie : mesure du d�sordre.
Unit� : J/K, joule par Kelvin.
Relations T/Q/S :
Q = m.c. (T2 � T1)
c :
capacit� calorique (ou capacit� thermique) qualit� d�un corps �
absorber/restituer de la chaleur par �change thermique lors d�une variation de
temp�rature.
En thermodynamique traditionnelle : S = Q/T
Affirmation 2
Oui.
Changement d��tat : la chaleur (l�apport d��nergie) est
enti�rement utilis�e pour modifier les liaisons mol�culaires (pas de variation
de temp�rature)
Chaleur latente : quantit� de chaleur pour r�aliser le
changement d��tat.
La figure repr�sente la variation d�entropie/temp�rature pour un
corps simple pur poss�dant une seule vari�t� allotropique (une seule forme
cristalline ou mol�culaire).
Noter les diff�rences de valeurs pour les chaleurs latentes de
fusion et d��bullition (Exemple pour l�eau pure).
�
Affirmation 3
Non.
Capacit� calorifique :
(ou capacit� thermique) qualit� d�un corps � absorber/restituer de la
chaleur
par �change thermique lors d�une variation de temp�rature.
Q = m.c. (T2 � T1)
Unit� :
joule par kelvin.
Les capacit�s caloriques de la glace, de l�eau et de la vapeur
d�eau n�ont pas les m�mes valeurs : les variations d��nergies �chang�es d�pendent
des �interactions
mol�culaires glace, eau, vapeur d�eau.�
Affirmation 4
Non.
[A].
L�int�grale de dT/T est ln, logarithme n�p�rien, de T2/T1.
Allotropique
Corps simple pur poss�dant une seule une seule forme
cristalline ou mol�culaire.
Le carbone est allotropique : il a plusieurs formes solides.
C(solide) graphite.
C(solide) diamant.
�
Page 11.
Variation de l�enthalpie
libre

S�lectionner l�affirmation exacte :
1- [A]. Diminution de l�enthalpie libre = r�action endothermique
2- [B]. A l��quilibre, ou en fin de r�action, l�enthalpie libre a
atteint sa valeur minimale et sa variation devient nulle
3- [C]. G devient sup�rieure � l�enthalpie libre
d��quilibre : impossible. � T & P constants, une r�action chimique �
l��quilibre ne peut pas sortir de l��quilibre
4- L�enthalpie libre G de d�part est toute l�enthalpie libre
disponible pour une r�action ou pour faire un travail
L�affirmation 2 est exacte.
Affirmation 1
Non.
[A]. Diminution de l�enthalpie libre = perte d��nergie =
r�action spontan�e exothermique.
Affirmation 3
Si.
[C]. Pour que l�enthalpie libre augmente et que la r�action de son
�quilibre, il faut faire un apport d��nergie ext�rieure.
Dans cette partie de courbe, *D rG > 0, =
r�action endothermique (n�cessite un apport d��nergie)
Affirmation 4
Non.
*D G (G de d�part � G final) est l��nergie libre disponible.
Le
signe de DG permet de pr�voir le sens d�une r�action.
Page 12.
Voir chimie
modifi�e/Documentation/2-Thermodynamique
Enthalpie G &
�quilibre chimique

S�lectionner l�affirmation exacte :
1- La position d��quilibre d�une r�action �quilibr�e ne d�pend pas
des concentrations
2- Le calcul de la constante d��quilibre ne peut se faire qu��
partir de l�entropie libre de r�action � l��quilibre
3- [A]. L�enthalpie libre est fonction de la temp�rature, de la
pression, de l�avancement de la r�action
4- [B]. Puisque la variation d�enthalpie libre � l��quilibre est
nulle, l�enthalpie standard de r�action est R.T.Ln k (signe positif)
L�affirmation 3 est exacte.
�
Affirmation 2
Non.
Le calcul de la constante d��quilibre peut aussi se faire � partir
des concentrations � l��quilibre.
Voir Loi d�action des masses
Affirmation 3
Oui.
[A]. L�enthalpie libre est fonction de la temp�rature, de la
pression, de l�avancement de la r�action.
L�avancement de r�action � ksi � �tant la diff�rence de
quantit�s d�une substance (n temps t � n initiale) / coefficient
st�chiom�trique.
On obtient le m�me avancement quel que soit l��l�ment de la r�action
consid�r�.
Le taux d�avancement (degr� d�avancement) = avancement � l�instant
t / avancement maximal.
Affirmation 4
Non.
[B].
Enthalpie standard de r�action est - R.T.Ln k (signe
n�gatif)
Pour comprendre : faire *D rGT,p = 0
dans la formule [A].
Page 13.
Calcul de l�enthalpie
libre

S�lectionner l�affirmation exacte :
1- [A]. La r�action est exothermique
2- Pour pr�voir le sens de la r�action : il faut calculer
l�enthalpie libre G de r�action
3- [B]. Variation d�enthalpie libre G positive = la r�action est
spontan�e
4- Ne poss�dant pas les concentrations, on ne peut pas d�finir la
constante d��quilibre k
L�affirmation 2 est exacte.
�
Affirmation 1
Non.
[A]. Augmentation de l�enthalpie : La r�action re�oit de la
chaleur = r�action endothermique.
La variation d�enthalpie (chaleur �chang�e) et la variation
d�entropie (variation du d�sordre) ne permettent pas de pr�voir le sens d�une
r�action.
Affirmation 3
Non.
[B]. Variation d�enthalpie libre G positive = la r�action n�est
pas spontan�e.
Affirmation 4
Si.
[C].
En utilisant la relation de Van�t Hoff ; relation entre
la variation de la constante d��quilibre � l��nergie de la r�action (en
fonction de la temp�rature)
A partir de l�enthalpie libre de r�action, [- *D G� = RT LnK],
calculer le Ln K,
puis k=elnK
Gaz
parfaits :
les mol�cules sont suffisamment �loign�es pour en n�gliger les interactions.
Exemples :
O2, N2 de l�atmosph�re.
R : constante des gaz parfaits = NA. KB = 8,3144621 J⋅K-1⋅mol-1
NA :
nombre d�Avogadro = 6,022 141 29(27)�1023 mol−1.
KB :
Constante de Boltzmann
Page 14.
Synth�se. Energies. Transformations
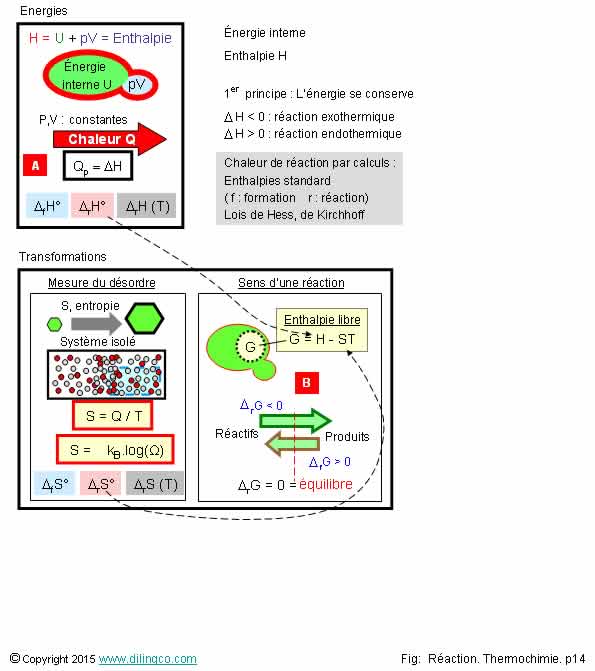
S�lectionner l�affirmation exacte :
1- [A]. Variation d�enthalpie � p constante = travail �chang� avec
l�ext�rieur
2- Dans un syst�me ferm� (inclus dans syst�me isol�), la variation
d�entropie est toujours positive
3- [B]. Calculer la variation d�enthalpie libre G permet de
pr�voir le sens d�une r�action
4- Entropie : Chaleur dissip�e lors d�une r�action
L�affirmation 2 est exacte.
�
Affirmation 1
Non.
[A]. Augmentation de l�enthalpie : La r�action re�oit de la
chaleur = r�action endothermique.
La variation d�enthalpie (chaleur �chang�e) et la variation
d�entropie (variation du d�sordre) ne permettent pas de pr�voir le sens d�une
r�action.
Affirmation 3
Non.
[B]. Variation d�enthalpie libre G positive = la r�action n�est
pas spontan�e.
Affirmation 4
Si.
[C].
En utilisant la relation de Van�t Hoff ; relation entre la
variation de la constante d��quilibre � l��nergie de la r�action (en fonction
de la temp�rature)
A partir de l�enthalpie libre de r�action, [-*DG� = RT LnK],
calculer le Ln K,
puis k=elnK
Gaz
parfaits :
les mol�cules sont suffisamment �loign�es pour en n�gliger les interactions.
Exemples :
O2, N2 de l�atmosph�re.
R : constante des gaz parfaits = NA. KB = 8,3144621 J⋅K-1⋅mol-1
NA :
nombre d�Avogadro = 6,022 141 29(27)�1023 mol−1.
KB :
Constante de Boltzmann
Les QCM interactifs sont accessibles � partir de la page d�accueil
du coaching virtuel � acc�s gratuit dilingco.com
Page 1.
Quelques d�finitions

S�lectionner les deux affirmations exactes :
1- Bouteille en plastique ferm�e : exemple de syst�me thermodynamique isol�
2- Une variable extensive est proportionnelle � la taille du syst�me
3- Les variables d��tat ont des valeurs qui d�pendent du chemin suivi pour atteindre l��tat consid�r�
4- La chaleur Q est une variable d��tat
5- Les variables d��tat sont ind�pendantes les unes des autres (Pas d��quation d��tat entre elles)
6- [A]. Fonction d��tat : ne d�pend que de l��tat syst�me consid�r�. Entre 2 �tats, ne d�pend pas du chemin suivi
7- Les transformations ne peuvent pas �tre d�finies en prenant une variable d��tat constante
Les affirmations 2 et 6 sont exactes.
�
Affirmation 1
Non.
Bouteille en plastique ferm�e : Syst�me thermodynamique ferm�.
Un syst�me thermodynamique ferm� peut �changer :
- un travail avec le milieu ext�rieur (la paroi est d�formable),
- de la chaleur avec le milieu ext�rieur.
Un syst�me ferm� ne peut pas d��change de mati�re avec le milieu ext�rieur.
Exemple de syst�me isol� (aucun �change avec le milieu ext�rieur) :
Bouteille thermos ferm�e id�ale ; pas d��change de mati�re, pas d��change d��nergie sous forme de chaleur, d��lectricit�, de travail (parois ind�formables) etc.
�
Affirmation 2
Oui.
Une variable extensive (d�pend de l�extension du syst�me) est proportionnelle � la taille du syst�me.
Exemples : nombre de moles, masse, volume, quantit� de chaleur Q
Les variables extensives peuvent s�additionner.
Exemple : Volume total = volume1 + volume2.
Une variable intensive ne d�pend pas de l�extension du syst�me, de la quantit� de mati�re.
Exemples :
Temp�rature T.
Unit� : degr� kelvin. O�k= -273,15 �C
Pression P. (Force par unit� de surface).
Unit� : pascal (1 N/M2) ou le bar 1 bar = 100 000 Pa
(Ancienne unit� : 1 atmosph�re = 1,01325.105 Pa)
Masse volumique (p ou�), masse par unit� de volume,
Concentration c, concentration massique, concentration molaire)
Fraction molaire x, proportion d�un composant dans un m�lange.
xi = ni / ntotal
Affirmation 3
Non.
Une variable d��tat caract�rise un �tat du syst�me.
Elle ne d�pend pas du chemin suivi pour atteindre l��tat
Principales grandeurs d��tat :
- Temp�rature T (mesure de l�agitation �lectronique � un instant donn�)
- Pression P
- Volume V, m3
- Energie interne U, J/kg
- Enthalpie H, J/kg
- Entropie S, J/k (joule par kelvin)
Affirmation 4
Non.
La chaleur Q :
- transfert d�sordonn� d��nergie thermique entre 2 syst�mes � temp�ratures diff�rentes,
- n�est pas une variable d��tat (d�pend du chemin choisi),
- unit� : (comme celle des autres �nergies) = joule.
Autre grandeur thermodynamique qui n�est pas une variable d��tat : le travail W, �nergie m�canique d�une force qui se d�place. Unit� : joule.
Affirmations 5
Non.
Les diff�rentes variables d��tat ne sont pas ind�pendantes entre elles.
Des � fonctions d��tat � ou � �quations d��tat � font ressortir les liens entre les variables d��tat.
Exemple : �quation des gaz parfaits.
(Gaz parfaits : les mol�cules sont suffisamment �loign�es pour en n�gliger les interactions).
�
Affirmation 6
Oui.
[A]. Fonction d��tat :
- ne d�pend que de l��tat syst�me consid�r�,
- si la fonction est �tablie entre 2 �tats, ne d�pend pas du chemin suivi.
La Loi d�Avogadro est une �quation d��tat :
Des volumes �gaux de gaz parfaits diff�rents, aux m�mes conditions de temp�rature et de pression, contiennent le m�me nombre de mol�cules.
Le nombre de moles :
- est proportionnel au volume consid�r�, proportionnel � la pression,
- inversement proportionnel � la temp�rature.
Note :
Gaz parfaits : les mol�cules sont suffisamment �loign�es pour en n�gliger les interactions.
Exemples : O2, N2 de l�atmosph�re.
R : constante des gaz parfaits = NA. KB = 8,3144621 J⋅K-1⋅mol-1
NA : nombre d�Avogadro = 6,022 141 29(27)�1023 mol−1.
KB : Constante de Boltzmann
Affirmation 7
Si.
Tr�s
souvent les transformations sont d�finies avec une variable d��tat constante.
Transformation isotherme : �
temp�rature constante
Isobare : � pression constante,
Isochore : � volume constant,
Isoenthalpique : � enthalpie constante,
Isoentropique : � entropie constante.
Adiabatique : pas d��change de chaleur avec le milieu ext�rieur.
Page 2.
Principes de la thermodynamique

S�lectionner les deux affirmations exactes :
1- [A]. 1
et 2 en �quilibre thermique, 2 et 3 en �quilibre thermique = Les trois syst�mes
sont en �quilibre thermique entre eux
2- [B]. Q2=Q1. L��nergie se conserve mais peut prendre des formes diff�rentes
3-
L��volution d�une r�action dans un syst�me isol� n�est jamais pr�dictible,
jamais irr�versible, et ne d�pend pas de consid�rations thermodynamiques
4- La thermodynamique s�int�resse aux processus de r�actions chimiques, � la
vitesse de r�action, aux fonctions et dur�es d��volutions
5- [C]. L��nergie d�un syst�me ferm� baisse : l��nergie du syst�me isol� qui le contient baisse aussi
Les affirmations 1 et 2 sont exactes.
Voir Physique, thermodynamique, Principes
Affirmation 1
Oui.
Principe 0 de la thermodynamique : Equilibre thermique.
Deux syst�mes en �quilibre thermique avec un troisi�me sont aussi en �quilibre thermique entre eux.
Affirmation 2
Oui
Principe
1 : L��nergie
se conserve.
L��nergie peut prendre des formes diff�rentes : agitation thermique
mol�culaire, travail m�canique, etc.
Pour un syst�me isol� :
Somme des diff�rentes formes d��nergies en Q2 = somme des formes d��nergies en Q1.
Affirmation 3
Si.
Deuxi�me principe : principe d��volution & d�entropie.
L��nergie passe irr�versiblement de formes concentr�es et potentielles, � des formes diffuses, d�sordonn�es, et cin�tiques.
Le
deuxi�me principe introduit la notion d�entropie.
L�entropie S est la mesure du d�sordre : Dans un
syst�me isol�, l�entropie (le d�sordre) augmente
de mani�re irr�versible.
En thermodynamique classique, l�unit� de l�entropie, quantit� de chaleur �chang�e par un syst�me, � temp�rature T constante, est le joule par kelvin.
Affirmation 5
Non.
Principe 1 : L��nergie se conserve.
Une perte en �nergie du syst�me interne va entra�ner une augmentation d��nergie
dans son milieu ext�rieur pour rester conforme, globalement, au deuxi�me
principe de la thermodynamique.
Q interne baisse => Q environnement augmente
(L��nergie diffus�e augmente l��nergie environnementale)
Q total = Q interne + Q environnement => augmente ou reste constante
- Reste constante si le syst�me global est en �quilibre ou �id�alement� proche de l��quilibre,
- Q ne peut pas diminuer : principe de la conservation de l��nergie d�un syst�me isol�.
Note :
Syst�me ferm� = permissible � l��nergie.
Principes de la thermodynamique
Quatre principes r�gissent la thermodynamique.
Le premier et le deuxi�me principe sont les plus importants.
- Principe 0 : �quilibre thermique
- Premier principe : principe de conservation de l��nergie.
L��nergie d�un syst�me isol� est constante ; Les formes de l��nergie peuvent varier (l��nergie se transforme)
- Deuxi�me principe : principe d��volution de l��nergie & entropie.
L��nergie passe irr�versiblement de formes : Concentr�es et potentielles, � des formes, diffuses, d�sordonn�es, et cin�tiques.
Le deuxi�me principe introduit la notion � d�entropie �.
L�entropie est la mesure du d�sordre d�un syst�me.
Le deuxi�me principe permet de pr�voir le sens d�une r�action chimique et� l��quilibre chimique d�une r�action.
- Troisi�me principe : un syst�me qui descend vers son �tat quantique fondamental voit sa temp�rature s�approcher du z�ro absolu
(O� Kelvin= - 273,15� C)
Page 3.
Entropie. Syst�me isol�

S�lectionner les deux affirmations exactes :
1- [A]. Un syst�me isol� atteint un �tat d'�quilibre lorsque son entropie S devient minimale
2- Transformation irr�versible : L�entropie globale (entropie interne du syst�me ferm� + entropie milieu ext�rieur) augmente
3- Dans un syst�me isol� l�entropie peut d�cro�tre
4- Un corps pur parfait, � la temp�rature absolue 0 Kelvin, est parfaitement ordonn�. Son entropie S est nulle
5- Les d�finitions de l�entropie S en thermodynamique classique, S=Q/T, et en thermodynamique statistique ([C]. Formule de Boltzmann), sont contradictoires
6- L�entropie n�est pas une variable d��tat
Les affirmations 2 et 4 sont exactes.
Voir Physique, thermodynamique, Entropie
Affirmation 1
Non.
[A] : Un syst�me atteint un �tat d'�quilibre lorsque son entropie S� devient maximale.
L�entropie S d�un syst�me isol� ne peut :�������
- qu�augmenter vers une valeur maximale, ou
- rester constante, autour de la valeur S maximale, lorsque un �quilibre est atteint (On dit alors que la transformation est r�versible).
On peut noter :
L�entropie refl�te la capacit� d�un syst�me � �voluer.
Plus l�entropie est faible, plus le syst�me peut �voluer.
Plus le syst�me �volue, moins il est capable d��voluer.
Affirmation 2
Oui.
[A] : Transformation irr�versible : il y a cr�ation globale d�entropie.
*D Sglobal = *D Ssyst + *D Sext >0
[B] : Transformation r�versible : la cr�ation d�entropie est nulle.
Dans le cas d�une �volution id�ale r�versible, on assume qu�il n�y a pas eu d��mission de chaleur, pas de pertes li�es aux frottements.
Quantit� de chaleur dissip�e Q = 0 donc la variation d�entropie S = 0
Affirmation 3
Non.
Syst�me isol� :
- pas d��change avec le milieu ext�rieur,
- l��nergie y est constante mais peut prendre des formes diff�rentes,
- Syst�me isol� : l�entropie ne peut pas d�cro�tre. Elle ne peut qu�augmenter ou rester constante si l��tat final est atteint.
Note :
Un syst�me non isol� peut avoir une variation d�entropie n�gative s�il produit une variation d�entropie positive sur son environnement.
Affirmation 4
Oui.
S = 0 � 0� K
Principe
de Nernst : L�entropie d�un cristal parfait � 0 kelvin est nulle.
Affirmation 5
Non.
Plusieurs interpr�tations de l�entropie sont possibles.
Les d�finitions de Clausius (S=Q/T) et de Boltzmann r�sultent de consid�ration du syst�me � des points de vues microscopique ou macroscopique du syst�me mais ne sont pas contradictoires.
Thermodynamique classique
S = entropie = Q/T
Q : quantit� de chaleur �chang�e par un syst�me, consid�r� dans son ensemble (au niveau macroscopique), � la temp�rature T.
Unit� : J/K, Joule par Kelvin
Thermodynamique statistique
L�entropie est la mesure du d�sordre d�un syst�me au niveau microscopique.
Plus l�entropie est grande :
- moins ses �l�ments sont ordonn�s, li�s entre eux,
- moins les �l�ments d�sordonn�s peuvent fournir de travail
(Ils gaspillent plus d��nergie pour fournir le travail).
S = kB.log(Ω)
kB est la constante de Boltzmann,
٠est le nombre d��tats
microscopiques dans le syst�me consid�r�.
Ω d�finit la complexit� du syst�me.
Plus le syst�me se d�sorganise au niveau microscopique, plus le nombre d��tats ٠est important (gigantesque !), plus l�entropie est grande.
Le nombre Ω ne peut pas �tre d�fini pour la plupart des syst�mes : l�entropie S ne peut pas ce calculer.
La thermodynamique statique s�applique � l�imagerie m�dicale par exemple.
Autres d�finitions de l�entropie
Informatique : entropie de Shannon,
Math�matique : entropie topologique, entropie m�trique.
Affirmation 6
Si.
L�entropie est une variable d��tat thermodynamique calculable dans l�absolue.
(Les autres ne peuvent �tre d�finie que par leurs variations)
Unit� de mesure : j/k, joule par kelvin, en thermodynamique classique.
Page 4
Enthalpie

S�lectionner les deux affirmations exactes :
1- Pression et volume sont des grandeurs intensives
2- La variation d�enthalpie au cours d�une r�action ne peut pas �tre mesur�e
3- La variation d�enthalpie lors d�une r�action ne d�pend pas des conditions ext�rieures
4- Lors d�une r�action, une diminution de l��nergie du syst�me = r�action exothermique
5- Variation d�enthalpie � pression constante = chaleur �chang�e => premier principe de la thermodynamique
6- Il faut apporter de la chaleur pour qu�une r�action exothermique (diminution de l�enthalpie) se fasse
Les affirmations 4 et 5 sont exactes.
Voir Physique, thermodynamique, Enthalpie
Affirmation 1
Non
pV d�pend du volume occup� par le
syst�me, c�est une grandeur extensive.
pV repr�sente le travail que le syst�me doit fournir contre la pression ext�rieure pour garder son volume.
Affirmation 2
Si.
La variation d�enthalpie (zone entour�e en rouge de la figure) correspond aux variations de chaleur Q fournie, ou re�ue, lors d�une r�action.
Mesurer la quantit� de chaleur �chang�e lors de la r�action revient � mesurer l�enthalpie.
Affirmation 3
Si.
*DH d�pend des conditions ext�rieures, des variations de l��nergie environnementale ; variations de pression ou de temp�rature, par exemples.
Affirmation 4
Oui.
Exothermique : La r�action fournie de la chaleur.
Endothermique : La r�action re�oit de la chaleur.
Athermique : pas d��change de chaleur
Isochore : � volume constant.
Isobare : � pression constante.
Isotherme : � temp�rature constante.
Affirmation 5
Oui.
*DH = Qp
Variation d�enthalpie = chaleur �chang�e (� pression constante)
Premier principe de la thermodynamique : L��nergie se conserve.
Affirmation 6
Non.
Il faut apporter de la chaleur pour qu�une r�action endothermique, qui consomme de l��nergie (variation d�enthalpie positive) se fasse.
Note :
Ceci d�montre une des utilit�s de la thermodynamique : pouvoir conna�tre, calculer l�enthalpie d�une r�action, permet de savoir s�il faut chauffer ou non pour qu�une r�action chimique se fasse.
A se rappeler
Enthalpie, du grec � chaleur interne � : chaleur (�nergie) interne + travail de maintient de volume. H = U + pV.
U :
�nergie interne emmagasin�e par le syst�me.
pV : travail pour maintenir le volume occup� par le syst�me.
� pv constant, variation d�enthalpie = chaleur �chang�e.
L�enthalpie = �nergie = dimension d�une �nergie.
Unit� : joule
Note :
La connaissance de l�enthalpie (li�e � la chaleur), permet, par exemples, de choisir le gaz le mieux appropri� pour chauffer un m�lange, chauffer ou refroidir pour augmenter le rendement d�une r�action chimique, etc.
Page 5.
Enthalpie libre G

S�lectionner les deux affirmations exactes :
1- Pour une r�action [r�actifs ->produits], la variation d'enthalpie libre est positive
2- Enthalpie libre G : partie de l�enthalpie utilisable pour produire une transformation chimique ou �lectrique
3- L�enthalpie libre G= H � TS n�est pas li�e au deuxi�me principe de la thermodynamique (�volution et entropie)
4- L�enthalpie libre G n�est ni une fonction d��tat ni une variable extensive
5- Syst�me riche en �nergie utilisable = enthalpie libre G de d�part �lev�e
Les affirmations 2 et 5 sont exactes.
Voir Physique, thermodynamique, Enthalpie libre G
Affirmation 1
Non.
R�action R�actifs -> Produits : variation d'enthalpie libre G diminue (*DG < 0).
Le signe de l�enthalpie libre permet de pr�voir le sens d�une r�action.
(Voir pages suivantes)
Affirmation 2
Oui.
Enthalpie libre G : partie de l�enthalpie utilisable pour produire une r�action chimique, �lectrique, ou un travail.
G : l�enthalpie libre G :
- introduite par Willard Gibbs,
- aussi appel� � �nergie de Gibbs �.
Affirmation 3
Si.
L�enthalpie libre G= H � TS est li�e au 2�me principe de la thermodynamique par sa variable S, entropie.
2�me principe de la thermodynamique : �volution et entropie.
Affirmation 4
Si.
La figure montre que l�enthalpie libre est li�e � un �tat du syst�me.
C�est aussi une grandeur extensible, par sa composante H li�e au volume.
Enthalpie H = U + pV
Enthalpie libre
L�enthalpie libre G, est aussi appel�e � �nergie libre de Gibbs �
G : Willard Gibbs.
G = H � TS
H : enthalpie
T : temp�rature en degr�s absolus dans l��chelle Kelvin
S : entropie
L�enthalpie libre peut �tre interpr�t�e comme la partie de l�enthalpie utilisable pour produire une transformation chimique ou �lectrique
(� temp�rature et � pression constante).
Variation d�enthalpie libre
Le syst�me �volue vers son �tat de plus faible �nergie.
Le signe de variation de l�enthalpie libre d�termine le sens de la r�action chimique.
R�actions � r�actifs vers produits � :
*D GT,p(sys) = *D H sys � T *D Ssys < 0�
R�actions � produits vers r�actifs � :
*D G T,p(sys) = *D H sys � T *D Ssys > 0�
R�action � l��quilibre :
*D G T,p(sys) = 0 = La r�action s�arr�te.
Page 6.
Enthalpies. Formation & r�action

S�lectionner l�affirmation exacte :
1- Les
enthalpies standard de formation des r�actifs et produits ne permettent pas de calculer
l�enthalpie standard d�une r�action
2- Les enthalpies standard de formation et de r�action sont pour T=273,15k (0�C) et P=1 atm
3- [B] : Tous les compos�s chimiques ont la m�me enthalpie standard de
formation
4- [A]. L�enthalpie standard de r�action permet de dire si la r�action est
exothermique, endothermique, ou adiabatique
L�affirmation 4 est exacte.
Affirmation
1
Si.
Le calcul de l�enthalpie standard d�une r�action est possible :
*D rH� = Somme des enthalpie de formation des produits � Somme des enthalpies
de formation des r�actifs.
Notes :
- Les coefficients stoechiom�triques entrent dans la formule.
- f = enthalpie de formation,
- r = enthalpie de la r�action,
- � = conditions standard.
Les enthalpies standard de formation des corps compos�s :
- sont d�finies dans des tables,
- peuvent �tre mesur�es exp�rimentalement.
Affirmation 3
Non.
[B]. L�enthalpie standard de formation, chaleur �chang�e lors de la r�action,
d�pend du compos� chimique obtenu.
L�enthalpie
standard de formation :
- not�e *D Hf�,
- variation
d�enthalpie lors de la formation du compos� � partir des corps simples purs,
- dans les conditions de l��tat standard
(p�= 1 bar = 105 Pa. T� = 298k (25�C),
- les corps simples purs doivent �tre dans un �tat stable (gaz ou liquide ou
solide) � l��tat standard,
- des
tables donnent des valeurs de l�enthalpie standard de formation pour les compos�s chimiques
principaux,
- les valeurs
peuvent aussi �tre mesur�es exp�rimentalement en r�alisant la r�action de
composition dans un calorim�tre et en mesurant la chaleur �chang�e.
Affirmation
4
Oui.
[A].
*D H = Qp
Variation d�enthalpie = chaleur �chang�e � pression constante.
Voir page pr�c�dente � Enthalpie �
La variation d�enthalpie standard de r�action permet de dire si la
r�action est :
- exothermique, *D rH < 0, il y a
perte de chaleur lors de la formation du compos� chimique,
- endothermique, *D rH > 0, la
r�action doit recevoir de la chaleur pour se faire,
- adiabatique, *D rH = 0,� pas d��change de chaleur lors de la r�action.
Page 7.
Enthalpies de formation.
Mesures

S�lectionner
l�affirmation exacte :
1- L�enthalpie de formation des corps compos�s ne peut pas �tre d�termin�e exp�rimentalement
2- Pas de relation entre la chaleur �chang�e et la variation de temp�rature
3- L'enthalpie de formation des corps simples (H2, O2, N2, etc), est par d�finition nulle
4- Pouvoir calorifique = capacit� calorifique
L�affirmation 3 est exacte.
Affirmation 1
Si.
Les enthalpies de formation peuvent �tre mesur�es en r�alisant la r�action dans un calorim�tre.
D�terminer la variation d�enthalpie revient � mesurer la variation de temp�rature, puis � d�terminer la chaleur �chang�e lors de la r�action de constitution du compos� chimique.
Notes :
- Calorim�tre : syst�me isol� destin� � mesurer les �changes de chaleur.
La mesure des variations de temp�rature permet de d�terminer l��change de chaleur et la variation d�enthalpie.
- Q = m.c. (T2 � T1)
- *D H
= Qp
Variation d�enthalpie = chaleur �chang�e � pression constante.
Voir page pr�c�dente � Enthalpie �
Affirmation 2
Si.
Relation entre chaleur �chang�e et la variation de temp�rature :
Q = m.c. (T2 � T1)
Q :
quantit� de chaleur en joules
m : masse en kg
c : capacit� calorifique
T : temp�rature en kelvin
Note :
- La capacit� calorifique (ou capacit� thermique) qualit� d�un corps � absorber/restituer de la chaleur par �change thermique lors d�une variation de temp�rature.
- on d�finit des capacit�s thermiques massiques cm, (j/kg/k), volumiques cv (j/m2/k), cm molaires (j/m/k).
Affirmation 3
Oui.
L'enthalpie de formation des corps simples (H2, O2, N2, etc), est par d�finition nulle : le corps simple pur n�a pas besoin d�une r�action de formation pour se former, pour se former � partir de lui-m�me.
Affirmation 4
Non.
Pouvoir calorifique :
(ou chaleur de combustion)
- notation : *D cH�,
- unit�s : kilojoule par kilogramme, kilojoule par mole, par litre
- enthalpie de r�action lors d�une combustion
Exemple : d�un hydrocarbure avec le dioxyg�ne.
Essence : 35 475 kj/L
Capacit� calorifique :
(ou capacit� thermique) qualit� d�un corps � absorber/restituer de la chaleur par �change thermique lors d�une variation de temp�rature.
Q = m.c. (T2 � T1)
Unit� :
joule par kelvin.
Page 8.
Table & calcul

S�lectionner
l�affirmation exacte :
1- [A]. Enthalpie molaire standard de r�action
2- [B]. Enthalpie de formation du graphite (carbone corps simple pur le plus stable aux conditions standard) : 1,92 kj/mole
3- [B]. La formation du diamant � partir du graphite n�cessite de la chaleur (1,92 kj/mole)
4- [C]. + 103,88
L�affirmation 3 est exacte.
Affirmation 1
Non. [A]. Enthalpie molaire standard de formation des compos�s chimiques de la premi�re colonne.
(Le � f � de *D fH0 signifie � formation �)
Notes :
La table pr�sent�e est une table simplifi�e.
Des tables d�enthalpies plus compl�tes se trouvent sur Internet.
L�enthalpie de formation d�un compos� peut toujours se d�terminer exp�rimentalement� (Voir calorim�tre page pr�c�dente).
Affirmation 2
Non.
[B]. Enthalpie de formation du graphite : 0 kj/mole.
Le graphite, carbone pur simple stable aux conditions standards (1pa,
25�C) n�a pas � se � former � en lui-m�me (C -> C).
Affirmation 3
[B].
Oui. La formation du diamant � partir du graphite n�cessite de la
chaleur.
Enthalpie de formation : 1,92 kj/mole.
Le
diamant n�est pas le carbone le plus stable aux conditions standard.
C(s) graphite -> C(s) diamant�� *D H0 = 1,9 kj/mole
Le carbone est allotropique : il a plusieurs formes solides.
Affirmation 4
Non.
[C]. *D fH0 du propane = - 103,88 (- = r�action
exothermique).
Loi de Hess = Somme des enthalpies de formation des produits � somme des
enthalpies de formation des r�actifs
Attention :
Respecter les signes dans les sommes et ne pas oublier les coefficients stoechiom�triques.
�
Page 9.
Enthalpie de r�action. T quelconque

S�lectionner l�affirmation exacte :
1- Conna�tre l�enthalpie standard de r�action et les capacit�s calorifiques ne permet pas de calculer l�enthalpie de r�action � T quelconque
2- L�enthalpie de la r�action de l�eau � 600�k est identique � celle � 298�k
3- � pression constante : Enthalpie de r�action = chaleur �chang�e
4- [A]. Il faut chauffer pour que la r�action se fasse
L�affirmation 3 est exacte.
Affirmation 1
Si.
Voir [A] loi de Kirchhoff.
Enthalpie de r�action � temp�rature T =
Enthalpie standard de r�action + enthalpie de T� � T
(A condition qu�il n�y ai pas de changement d��tat entre les 2 temp�ratures)
Enthalpie de T� � T =
Coeff. Stoechiom�trique x capacit� calorique x DT
Capacit� calorifique :
(ou capacit� thermique) qualit� d�un corps � absorber/restituer de la chaleur par �change thermique lors d�une variation de temp�rature.
Q = m.c. (T2 � T1)
Unit� :
joule par kelvin.
Affirmation 2
Non.
L�enthalpie
de r�action d�pend :
- de la temp�rature de la r�action,
- de la phase (gaz, liquide, solide) o� sont les composants.
L�enthalpie de la r�action de l�eau � 600�k = -245,1 kj.mol-1
L�enthalpie de la r�action de l�eau � 298�k = -241,6 kj.mol-1
Affirmation3
Oui.
� pression constante : *D H = Qp
Enthalpie de r�action = chaleur �chang�e
Affirmation 4
Non.
[A]. Perte de chaleur, la r�action est exothermique.
Page 10.
Changement d��tats
La figure pr�sente l��volution de l�entropie pour un corps pur allotropique (Ici, l�eau pure).

S�lectionner l�affirmation exacte :
1- Pas de lien entre l�entropie, la chaleur, la temp�rature
2- Changement d��tat : la chaleur est enti�rement utilis�e pour modifier les liaisons mol�culaires (pas de variation de temp�rature)
3- Les capacit�s caloriques de la glace, de l�eau, de la vapeur d�eau, ont les m�mes valeurs
4- [A]. Variation d�entropie entre Tf et T2 : L�int�grale de dT/T est Log d�cimal de T2/Tf
L�affirmation 2 est exacte.
Affirmation 1
Si.
T. Temp�rature : variable d��tat. Mesure de l�agitation �lectronique.
Unit� : � kelvin.
Q.
Chaleur :
transfert d��nergie entre 2 syst�mes � temp�ratures diff�rentes. Se mesure en
joules.
En dehors des changements d��tats : l��nergie re�ue fait cro�tre l�agitation �lectronique et donc la temp�rature.
S. Entropie : mesure du d�sordre.
Unit� : J/K, joule par Kelvin.
Relations T/Q/S :
Q = m.c. (T2 � T1)
c :
capacit� calorique (ou capacit� thermique) qualit� d�un corps �
absorber/restituer de la chaleur par �change thermique lors d�une variation de
temp�rature.
En thermodynamique traditionnelle : S = Q/T
Affirmation 2
Oui.
Changement d��tat : la chaleur (l�apport d��nergie) est enti�rement utilis�e pour modifier les liaisons mol�culaires (pas de variation de temp�rature)
Chaleur latente : quantit� de chaleur pour r�aliser le changement d��tat.
La figure repr�sente la variation d�entropie/temp�rature pour un corps simple pur poss�dant une seule vari�t� allotropique (une seule forme cristalline ou mol�culaire).
Noter les diff�rences de valeurs pour les chaleurs latentes de fusion et d��bullition (Exemple pour l�eau pure).
�
Affirmation 3
Non.
Capacit� calorifique :
(ou capacit� thermique) qualit� d�un corps � absorber/restituer de la chaleur par �change thermique lors d�une variation de temp�rature.
Q = m.c. (T2 � T1)
Unit� :
joule par kelvin.
Les capacit�s caloriques de la glace, de l�eau et de la vapeur d�eau n�ont pas les m�mes valeurs : les variations d��nergies �chang�es d�pendent des �interactions mol�culaires glace, eau, vapeur d�eau.�
Affirmation 4
Non.
[A].
L�int�grale de dT/T est ln, logarithme n�p�rien, de T2/T1.
Allotropique
Corps simple pur poss�dant une seule une seule forme cristalline ou mol�culaire.
Le carbone est allotropique : il a plusieurs formes solides.
C(solide) graphite.
C(solide) diamant.
�
Page 11.
Variation de l�enthalpie libre

S�lectionner l�affirmation exacte :
1- [A]. Diminution de l�enthalpie libre = r�action endothermique
2- [B]. A l��quilibre, ou en fin de r�action, l�enthalpie libre a atteint sa valeur minimale et sa variation devient nulle
3- [C]. G devient sup�rieure � l�enthalpie libre d��quilibre : impossible. � T & P constants, une r�action chimique � l��quilibre ne peut pas sortir de l��quilibre
4- L�enthalpie libre G de d�part est toute l�enthalpie libre disponible pour une r�action ou pour faire un travail
L�affirmation 2 est exacte.
Affirmation 1
Non.
[A]. Diminution de l�enthalpie libre = perte d��nergie = r�action spontan�e exothermique.
Affirmation 3
Si.
[C]. Pour que l�enthalpie libre augmente et que la r�action de son �quilibre, il faut faire un apport d��nergie ext�rieure.
Dans cette partie de courbe, *D rG > 0, = r�action endothermique (n�cessite un apport d��nergie)
Affirmation 4
Non.
*D G (G de d�part � G final) est l��nergie libre disponible.
Le
signe de DG permet de pr�voir le sens d�une r�action.
Page 12.
Voir chimie modifi�e/Documentation/2-Thermodynamique
Enthalpie G & �quilibre chimique

S�lectionner l�affirmation exacte :
1- La position d��quilibre d�une r�action �quilibr�e ne d�pend pas des concentrations
2- Le calcul de la constante d��quilibre ne peut se faire qu�� partir de l�entropie libre de r�action � l��quilibre
3- [A]. L�enthalpie libre est fonction de la temp�rature, de la pression, de l�avancement de la r�action
4- [B]. Puisque la variation d�enthalpie libre � l��quilibre est nulle, l�enthalpie standard de r�action est R.T.Ln k (signe positif)
L�affirmation 3 est exacte.
�
Affirmation 2
Non.
Le calcul de la constante d��quilibre peut aussi se faire � partir des concentrations � l��quilibre.
Voir Loi d�action des masses
Affirmation 3
Oui.
[A]. L�enthalpie libre est fonction de la temp�rature, de la pression, de l�avancement de la r�action.
L�avancement de r�action � ksi � �tant la diff�rence de quantit�s d�une substance (n temps t � n initiale) / coefficient st�chiom�trique.
On obtient le m�me avancement quel que soit l��l�ment de la r�action consid�r�.
Le taux d�avancement (degr� d�avancement) = avancement � l�instant t / avancement maximal.
Affirmation 4
Non.
[B].
Enthalpie standard de r�action est - R.T.Ln k (signe n�gatif)
Pour comprendre : faire *D rGT,p = 0 dans la formule [A].
Page 13.
Calcul de l�enthalpie libre

S�lectionner l�affirmation exacte :
1- [A]. La r�action est exothermique
2- Pour pr�voir le sens de la r�action : il faut calculer l�enthalpie libre G de r�action
3- [B]. Variation d�enthalpie libre G positive = la r�action est spontan�e
4- Ne poss�dant pas les concentrations, on ne peut pas d�finir la constante d��quilibre k
L�affirmation 2 est exacte.
�
Affirmation 1
Non.
[A]. Augmentation de l�enthalpie : La r�action re�oit de la chaleur = r�action endothermique.
La variation d�enthalpie (chaleur �chang�e) et la variation d�entropie (variation du d�sordre) ne permettent pas de pr�voir le sens d�une r�action.
Affirmation 3
Non.
[B]. Variation d�enthalpie libre G positive = la r�action n�est pas spontan�e.
Affirmation 4
Si.
[C].
En utilisant la relation de Van�t Hoff ; relation entre la variation de la constante d��quilibre � l��nergie de la r�action (en fonction de la temp�rature)
A partir de l�enthalpie libre de r�action, [- *D G� = RT LnK],
calculer le Ln K,
puis k=elnK
Gaz parfaits : les mol�cules sont suffisamment �loign�es pour en n�gliger les interactions.
Exemples : O2, N2 de l�atmosph�re.
R : constante des gaz parfaits = NA. KB = 8,3144621 J⋅K-1⋅mol-1
NA : nombre d�Avogadro = 6,022 141 29(27)�1023 mol−1.
KB : Constante de Boltzmann
Page 14.
Synth�se. Energies. Transformations

S�lectionner l�affirmation exacte :
1- [A]. Variation d�enthalpie � p constante = travail �chang� avec l�ext�rieur
2- Dans un syst�me ferm� (inclus dans syst�me isol�), la variation d�entropie est toujours positive
3- [B]. Calculer la variation d�enthalpie libre G permet de pr�voir le sens d�une r�action
4- Entropie : Chaleur dissip�e lors d�une r�action
L�affirmation 2 est exacte.
�
Affirmation 1
Non.
[A]. Augmentation de l�enthalpie : La r�action re�oit de la chaleur = r�action endothermique.
La variation d�enthalpie (chaleur �chang�e) et la variation d�entropie (variation du d�sordre) ne permettent pas de pr�voir le sens d�une r�action.
Affirmation 3
Non.
[B]. Variation d�enthalpie libre G positive = la r�action n�est pas spontan�e.
Affirmation 4
Si.
[C].
En utilisant la relation de Van�t Hoff ; relation entre la variation de la constante d��quilibre � l��nergie de la r�action (en fonction de la temp�rature)
A partir de l�enthalpie libre de r�action, [-*DG� = RT LnK],
calculer le Ln K,
puis k=elnK
Gaz parfaits : les mol�cules sont suffisamment �loign�es pour en n�gliger les interactions.
Exemples : O2, N2 de l�atmosph�re.
R : constante des gaz parfaits = NA. KB = 8,3144621 J⋅K-1⋅mol-1
NA : nombre d�Avogadro = 6,022 141 29(27)�1023 mol−1.
KB : Constante de Boltzmann