Les QCM interactifs sont accessibles à partir de la page d’accueil
du coaching virtuel à accès gratuit dilingco.com
Page
1.
Couple Acide Base

Sélectionner
les deux affirmations exactes :
1- [A]. pH
= - log [ions hydroxyde]
2- [B]. pH
d’une solution = pKa du couple acide base + logarithme [Acide]/[Base]
3- [C]. Valeur
de la constante d’autoprotolyse de l’eau Ke : 7
4- Acide
fort : constant d’acidité ka forte (ou pka petit ou négatif)
5-
Calculer le pH d’une solution = trouver la concentration [oxonium] car pH=
- log [Oxonium]
6- [Oxonium]=
0,000 001 mol/L : pH= - 6
7- 0,0001
mol/L d’H2SO4 (acide fort, pka= -3 ; dissociation complète) : pH=3
Les affirmations
4 et 5 sont exactes.
Les formules présentées doivent être toutes comprises et retenues.
Revoir
Coupe acide base
Affirmation
1
Non.
[A]. pH=
- log [ions oxonium]
Le pH
caractérise la concentration d’ions [H3O+]
solvatés dans la solution).
Si [Acide] = [Base] : log ([Base]/[Acide]) = log 1 = 0, pH = pKa
Autoprotolyse
de l’eau :
Oxonium
= H3O+
Hydroxyde=
HO-
Hydronium
(H9O4+), Oxonium solvaté.
Affirmation 2
Non.
pH = pKa + logarithme décimal du rapport des concentrations base acide. (Et non [Acide]/[Base])
pH = pka + log ([Base]/[Acide])
Affirmation
3
Non.
[C]. à
25°C, la constante d’autoprotolyse de l’eau Ke = 10-14.
L'eau
pure est neutre : autant d’ions hydronium que d’ions oxonium.
[OH-] = [H3O+] = 10-7 mole par litre à 25°C.
pH = -log [H3O+] = 7 = pH neutre.
Affirmation
4
Oui.
Acide fort : ka constant d’acidité forte, l’acide
AH s’est totalement dissocié en ions H3O+ et
en base conjuguée A-.
pka = - log10 Ka : petit ou négatif.
Base
forte : Kb grand, beaucoup d’ions hydronium
(Donc
peut d’ion oxonium : c'est à dire Ka petit)
Affirmation
5
Oui.
Calculer
le pH d’une solution = trouver la concentration [oxonium] car pH= - log [H3O+].
Affirmation
6
Non.
[Oxonium]=
0,000001 mol/L : pH= - log 10-6
= plus 6
Affirmation
7
Non.
Le pKa
est lié à la qualité de l’acide. Pka = -3 = acide fort.
Le pH est
la concentration d’[H3O+] obtenue en versant l’élément, en concentration 0,0001
mol/L, dans la solution.
Une mole d’H2SO4
se dissocie en 2 moles de protons H+
et une mole de SO4-. (Ne pas oublier les coefficients
stoechiométriques)
0,0001
mol/L d’H2SO4 = 0,0002 mol/L d’H3O+
pH=
- log 2.10-4 = 3,6
Notes
L’acidité d’une solution augmente quand le pH diminue
(Quand la concentration H3O+ augmente)
L’eau est le solvant, elle n’apparaît pas ni dans la formule de la constante
d’acidité Ka, ni dans la formule de la constante de basicité Kb.
Ka, constante d’acidité, est le nom donné à la constante
d’équilibre K dans le cas d’une réaction de dissociation acide base.
Conformément
à la loi d’action des masses, Ka exprime le rapport produits/réactifs d’une dissociation
à l’équilibre d’un acide AH avec une base H2O. L’eau, solvant,
n’apparaît pas dans la formule.
Dans les
calculs, on suppose que l’activité des espèces chimiques est optimale et
n’intervient pas (les concentrations n’ont pas à être multipliées par un
coefficient inférieur à 1).
Page 2.
Relations pH [Oxonium]
[Hydroxyle]

Sélectionner
les deux affirmations exactes :
1- H2SO4,
acide fort, concentré à 0,01 mole/L : pH & pka= -2
2- [A].
2,4 est un pH
3- [B].
Résultat correct (Logarithme décimal de 1.10 puissance moins 11 = 11)
4- [C].
Concentration en ions oxonium : log [pH]
5-
Solution de base forte à 0,1 mol/L : concentration en ions oxonium = Ke/0,1
6- Si
[Oxonium]= 0,0001 mol/L, le pH est : -4, la solution est très basique
Les
affirmations 3 et 5 sont exactes.
Affirmation
1
Non.
1)- H2SO4,
acide fort, concentré à 0,01 mole/L :
pH = - Log(0.01)
= -(-2) = 2
(et non
-2, ne pas oublier le « -log »)
2)- H2SO4
est un acide fort, son pka = -3
(Ne pas
confondre pka et pH)
H2SO4 => pka : -3, ph de la
solution : 2
(2, du
fait de la concentration)
Affirmation
2
Non.
[A].
Logarithme
décimal d’une concentration d’ions H3O+
pour trouver un pH.
pH=-log[H3O+]
Affirmation
4
Non.
[C].
Concentration ions oxonium = 10-pH
Affirmation
5
Oui.
Base
forte = complètement dissociée en ion hydronium HO-
[HO-]
= [Base forte initiale] = 0,1 mol/L
Ke=
10-14 = [H3O+].[10-1]
[H3O+]=
10-14 / 10-1 = 10-13
Ke: Constante
de dissociation de l’eau
Affirmation
6
Non.
Concentration
[H3O+]= 0,0001 mol/L.
pH = -
log 10-4 = +4
(Inférieur
à 7, la solution est faiblement acide).
Démarche
inverse :
pH=2
[H2O+]
= 1O^-pH = 10-2 mol/L
Page 3.
Ke. Ka. Kb. pH. pKe

Sélectionner
l’affirmation exacte :
1-
[A]. ke = log Ka . log kb
2- La
concentration [HO-] d’une solution 0,01 mol/L, le pH de la solution est pH = 2
3- pKa
ammoniac = 9,2 : L’ammoniac est une base forte. Elle se dissocie
entièrement en solution aqueuse
4- [B]. pKb
= pke–pka = 14–9,2 = 4,8
L’affirmation
4 est exacte.
Affirmation
1
Non.
[A]. ke = Ka . kb
Affirmation
2
Non.
pH
= pKe + log [HO-] = 14 + log [HO-] = 14 + log (0,01) = 14 - 2 = 12
Affirmation
3
Non.
pKa
ammoniac = 9,2
- > 7 : base
- << 14 : base faible
Une base faible, comme un acide faible, se dissocient
partiellement en solution aqueuse.
Page 4.
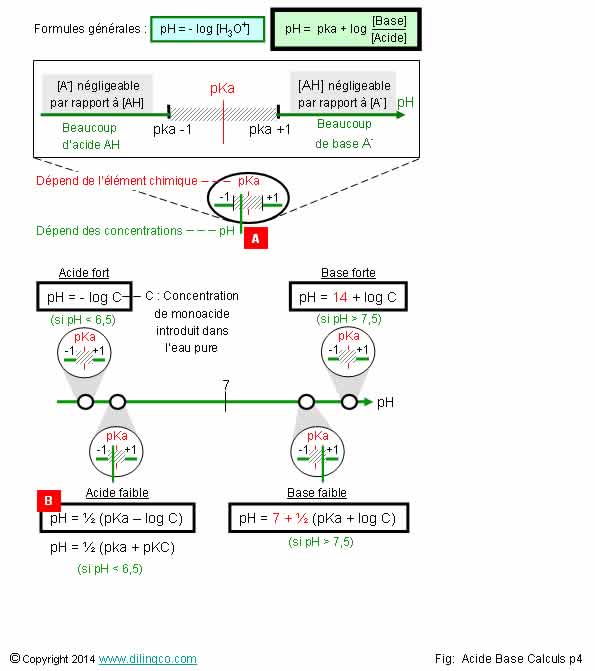
Formules approchées
Sélectionner
l’affirmation exacte :
1- [A].
Exemple : pH < pka : la base reste prédominante
2- [B].
La relation n’est pas égale à : pH = ½ (pka + pKC)
3- Acides
et bases faibles : des coefficients ½ apparaissent dans les relations
4- Pas la
peine de vérifier, en fin de calculs, que les ions oxonium provenant de
l’autoprotolyse de l’eau, sont en concentrations négligeables
L’affirmation
3 est exacte.
Affirmation
1
Non.
[A].
Exemple : pH < pka : l’acide reste
prédominant.
Affirmation
2
Si.
[B]. La
relation pH=1/2 (pKa-logC) peut aussi
s’écrire :
pH = ½ (pka + pKC), puisque pKC = - log C
pKC,
potentiel chimique de l’élément C introduit en concentration C.
Affirmation
4
Si.
En fin de
calculs, vérifier que le pH trouvé indique que les ions oxonium provenant de
l’autoprotolyse de l’eau sont en concentrations négligeables.
C’est le cas si :
- pour un
acide, pH calculé est intérieur à 6,5
- pour une
base, pH calculé est supérieur à 7,5
- Bases
et acides forts. Conditions de validité des relations approchées.
[Concentration]
>à 10-5 mol/L
(Les concentrations en acide fort ou en base forte ne doivent
pas être trop faibles).
- Acides et
bases faibles. Conditions de validité des relations approchées :
1 mol/L
< [Concentration] < 10-6 mol/L
- Partant
de la relation de base pH = pka + log ([Base] /
[Acide]) on peut prouver la justesse des relations approchées utilisées
pour les calculs.
(Faire une recherche Internet)
Page 5.
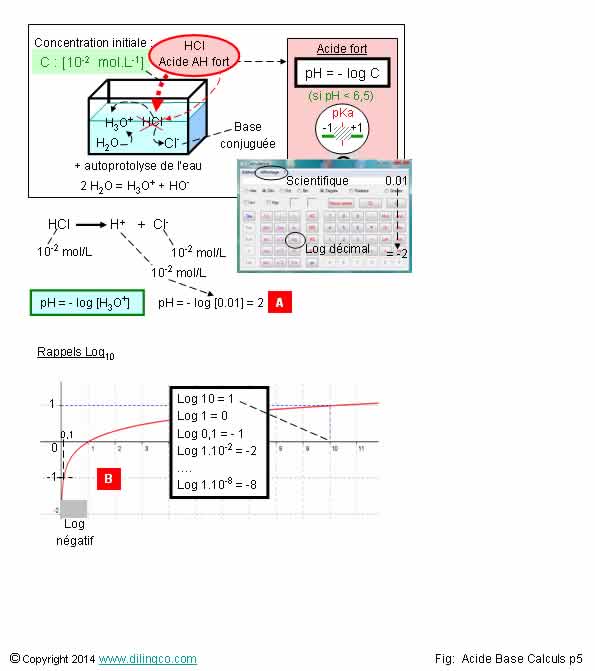
Calcul pH. Acide fort
Sélectionner
l’affirmation exacte :
1- [A]. pH
= 2 : L’acide chlorhydrique est un acide faible
2-
[B]. Log [1]=0, Log
[0,1]=-2, Log [0,01]=-3, Log [10^7]=7
3- Le
logarithme décimal des nombres inférieurs à 1 sont positifs
4- Les
coefficients stoechiométriques n’entrent pas dans le calcul pH=-log
[concentration]
L’affirmation
2 est exacte.
Affirmation
1
Non.
Ne pas
confondre le pH et le pKa.
Le pKa de
l’acide chlorhydrique = -3 (voir tables de pKa) :
acide fort.
(Acides
forts, pka < -2)
Le pH est le -log de la concentration d’H3O+ dans la solution.
Le pH
dépend de la concentration, de la température, et caractérise l’état plus ou
moins acide de la solution.
Affirmation
2
Oui.
[B].
Log [1]=0,
Log
[0,1]=-2, Log [0,01]=-3, Log [10^7]= 7
Le logarithme décimal est le nombre de fois dont un nombre doit
être multiplié
pour obtenir le nombre voulu. C’est un exposant.
Exemple :
10 000 000
= 10^7 = 10 puissance 7 = 10x10x10x10x10x10x10
Log10
10 000 000 = 7
Il faut
multiplier sept fois pour obtenir 10 000
000.
Affirmation
3
Non.
Les
logarithmes décimaux des nombres inférieurs à 1 sont négatifs.
Affirmation
4
Si.
Les
coefficients stoechiométriques entrent dans le calcul
pH=-log [coeff x concentration]
Exemple :
H2SO4
-> 2 H+ + SO4-
0,1 mole
d’acide donne 2 x 0,1 moles de
protons et 0,1 mole de base associée.
pH = -
log [2 x 0,1]
(Multiplier
la concentration par son coefficient stoechiométrique)
Acide
fort : complètement dissocié en proton H+ et
en base associée.
Sont
considérés acides forts les acides à partir de pka
= -2
[H+] = [AH] initiale
[AH]
finale = 0
pH = - log [H+]
Page 6.
Calcul pH. Base forte

Sélectionner
les deux affirmations exactes :
1- [Base
forte initiale] = Concentration finale ions H3O+
2- KOH =
base, donc : KOH + H => KOH2
3- La
soude, hydroxyde de sodium NaOH, ou la potasse, hydroxyde de potassium KOH sont
des exemples de bases fortes
4- [A]. pH
= - log 0,25 = 0,6
5- [B].
Attention, KOH est un complexe. Il se dissocie directement en ions K et ions
HO-, sans former d’acide conjugué
6- [B].
Si l’on dilue 10 fois la solution, le pH sera divisé par 10
Les affirmations
3 et 5 sont exactes.
Affirmation
1
Non.
[OH-]
= [Base]0
Concentration
finale ions hydroxyles HO- =
[Base forte initiale]
Une base forte se dissocie presque complètement HO- et
en acide conjugué BH.
Affirmation
2
Non.
KOH est une base mais aussi un « complexe ».
Les
complexes se dissocient dans l’eau, « Réaction de complexation ».
KOH + H2O => K+
+ H2O + OH-
Affirmation
4
Non.
[A].
La
dissociation d’une [base] donne des
ions hydroxyles [HO-].
Le pH est le –log [H3O+].
il faut trouver la concentration des ions oxonium à partir de la concentration
des hydroxyles.
Ke= [HO-].[H3O+]=14^-14
Et pOH=- log[HO-]
Dans le
cas d’une base, pH = Ke – pOH = 14 – log 0,25 = 14 - 0,6 = 13,4
Affirmation
6
Non.
[B]. Si
l’on dilue 10 fois la solution, refaire les calculs, comme présents réponse 4,
en prenant la concentration divisée par 10 :
0,5 10-2 mol/L.
Page 7.
Calcul pH. Acide faible

Sélectionner
l’affirmation exacte :
1-
Formule approchée pour le calcul du pH d’un acide faible : pH= pka+logC
2- [A].
pH = 1,5
3- [A].
On peut utiliser la formule des acides faibles pour 2 raisons : on nous
dit que pka = 4 (= acide faible) et le pH trouvé est plus petit que 4-1
4- [B].
L’acide AH s’est entièrement dissocié
L’affirmation
3 est exacte.
Affirmation
1
Non.
pH = ½ (pKa – logC0)
pKC0=
-logC0
pH = ½ (pKa + pkC0)
C0 :
concentration initiale d’acide.
Formules à savoir par coeur.
Affirmation
4
Non.
[B]. Seulement 62% des moles initiales d’acide se sont
dissociées : l’acide est un acide
faible.
Concentration oxonium à partir du pH :
[H3O+]=
10^-3,2 = 0,0062 mol.L-1
Calcul du pka à partir du pH et de la concentration initiale:
3,2
= 1/2pka -1/2 logC0 = ½ pka - ½Log 0,01 = ½ pka +1
pka=
4,4
Page 8.
Calcul pH. Base faible

Sélectionner
l’affirmation exacte :
1- Acides
et bases : même formule de calculs approchés du pH
2- [A]. Base :
espèce chimique qui en solution donne des ions hydroxydes HO-
3- pKa =
9,2 : base forte
L’affirmation
2 est exacte.
Affirmation
1
Non.
Acide
faible : pH = ½ (pka + pkC)
Base
faible : pH = ½ (pke + pka – pkc)
Affirmation
2
Oui.
Base :
espèce chimique qui en solution donne des ions hydroxydes HO-
Les ions
HO- peuvent provenir :
- de la
dissociation de la base : BOH
-> B+ + HO-
-
de la décomposition de H2O : A- + H2O -> AH + HO-
Affirmation
3
Non.
pKa =
9,2 : base faible.
Bases fortes : pKa = 14 et plus.
Exemples
de bases fortes : Oxyde de sodium-hydroxyde de sodium (Na2O,
NaOH), oxyde de potassium-hydroxyde de potassium (K2O,KOH), oxyde de
calcium-hydroxyde de calcium (CaO, Ca(OH)2), O2-,
...
Les QCM interactifs sont accessibles à partir de la page d’accueil
du coaching virtuel à accès gratuit dilingco.com
Page 1.
Couple Acide Base

Sélectionner les deux affirmations exactes :
1- [A]. pH = - log [ions hydroxyde]
2- [B]. pH d’une solution = pKa du couple acide base + logarithme [Acide]/[Base]
3- [C]. Valeur de la constante d’autoprotolyse de l’eau Ke : 7
4- Acide fort : constant d’acidité ka forte (ou pka petit ou négatif)
5- Calculer le pH d’une solution = trouver la concentration [oxonium] car pH= - log [Oxonium]
6- [Oxonium]= 0,000 001 mol/L : pH= - 6
7- 0,0001 mol/L d’H2SO4 (acide fort, pka= -3 ; dissociation complète) : pH=3
Les affirmations 4 et 5 sont exactes.
Les formules présentées doivent être toutes comprises et retenues.
Revoir Coupe acide base
Affirmation 1
Non.
[A]. pH= - log [ions oxonium]
Le pH caractérise la concentration d’ions [H3O+] solvatés dans la solution).
Si [Acide] = [Base] : log ([Base]/[Acide]) = log 1 = 0, pH = pKa
Autoprotolyse de l’eau :
Oxonium = H3O+
Hydroxyde= HO-
Hydronium (H9O4+), Oxonium solvaté.
Affirmation 2
Non.
pH = pKa + logarithme décimal du rapport des concentrations base acide. (Et non [Acide]/[Base])
pH = pka + log ([Base]/[Acide])
Affirmation 3
Non.
[C]. à 25°C, la constante d’autoprotolyse de l’eau Ke = 10-14.
L'eau pure est neutre : autant d’ions hydronium que d’ions oxonium.
[OH-] = [H3O+] = 10-7 mole par litre à 25°C.
pH = -log [H3O+] = 7 = pH neutre.
Affirmation 4
Oui.
Acide fort : ka constant d’acidité forte, l’acide AH s’est totalement dissocié en ions H3O+ et en base conjuguée A-.
pka = - log10 Ka : petit ou négatif.
Base forte : Kb grand, beaucoup d’ions hydronium
(Donc peut d’ion oxonium : c'est à dire Ka petit)
Affirmation 5
Oui.
Calculer le pH d’une solution = trouver la concentration [oxonium] car pH= - log [H3O+].
Affirmation 6
Non.
[Oxonium]= 0,000001 mol/L : pH= - log 10-6 = plus 6
Affirmation 7
Non.
Le pKa est lié à la qualité de l’acide. Pka = -3 = acide fort.
Le pH est
la concentration d’[H3O+] obtenue en versant l’élément, en concentration 0,0001
mol/L, dans la solution.
Une mole d’H2SO4
se dissocie en 2 moles de protons H+
et une mole de SO4-. (Ne pas oublier les coefficients
stoechiométriques)
0,0001 mol/L d’H2SO4 = 0,0002 mol/L d’H3O+
pH= - log 2.10-4 = 3,6
Notes
L’acidité d’une solution augmente quand le pH diminue
(Quand la concentration H3O+ augmente)
L’eau est le solvant, elle n’apparaît pas ni dans la formule de la constante d’acidité Ka, ni dans la formule de la constante de basicité Kb.
Ka, constante d’acidité, est le nom donné à la constante
d’équilibre K dans le cas d’une réaction de dissociation acide base.
Conformément
à la loi d’action des masses, Ka exprime le rapport produits/réactifs d’une dissociation
à l’équilibre d’un acide AH avec une base H2O. L’eau, solvant,
n’apparaît pas dans la formule.
Dans les calculs, on suppose que l’activité des espèces chimiques est optimale et n’intervient pas (les concentrations n’ont pas à être multipliées par un coefficient inférieur à 1).
Page 2.
Relations pH [Oxonium] [Hydroxyle]

Sélectionner les deux affirmations exactes :
1- H2SO4, acide fort, concentré à 0,01 mole/L : pH & pka= -2
2- [A]. 2,4 est un pH
3- [B]. Résultat correct (Logarithme décimal de 1.10 puissance moins 11 = 11)
4- [C]. Concentration en ions oxonium : log [pH]
5- Solution de base forte à 0,1 mol/L : concentration en ions oxonium = Ke/0,1
6- Si [Oxonium]= 0,0001 mol/L, le pH est : -4, la solution est très basique
Les affirmations 3 et 5 sont exactes.
Affirmation 1
Non.
1)- H2SO4, acide fort, concentré à 0,01 mole/L :
pH = - Log(0.01) = -(-2) = 2
(et non -2, ne pas oublier le « -log »)
2)- H2SO4 est un acide fort, son pka = -3
(Ne pas confondre pka et pH)
H2SO4 => pka : -3, ph de la solution : 2
(2, du fait de la concentration)
Affirmation 2
Non.
[A].
Logarithme décimal d’une concentration d’ions H3O+ pour trouver un pH.
pH=-log[H3O+]
Affirmation 4
Non.
[C]. Concentration ions oxonium = 10-pH
Affirmation 5
Oui.
Base forte = complètement dissociée en ion hydronium HO-
[HO-] = [Base forte initiale] = 0,1 mol/L
Ke= 10-14 = [H3O+].[10-1]
[H3O+]= 10-14 / 10-1 = 10-13
Ke: Constante de dissociation de l’eau
Affirmation 6
Non.
Concentration [H3O+]= 0,0001 mol/L.
pH = - log 10-4 = +4
(Inférieur à 7, la solution est faiblement acide).
Démarche inverse :
pH=2
[H2O+] = 1O^-pH = 10-2 mol/L
Page 3.
Ke. Ka. Kb. pH. pKe

Sélectionner l’affirmation exacte :
1- [A]. ke = log Ka . log kb
2- La concentration [HO-] d’une solution 0,01 mol/L, le pH de la solution est pH = 2
3- pKa ammoniac = 9,2 : L’ammoniac est une base forte. Elle se dissocie entièrement en solution aqueuse
4- [B]. pKb = pke–pka = 14–9,2 = 4,8
L’affirmation 4 est exacte.
Affirmation 1
Non.
[A]. ke = Ka . kb
Affirmation 2
Non.
pH = pKe + log [HO-] = 14 + log [HO-] = 14 + log (0,01) = 14 - 2 = 12
Affirmation 3
Non.
pKa ammoniac = 9,2
- > 7 : base
- << 14 : base faible
Une base faible, comme un acide faible, se dissocient partiellement en solution aqueuse.
Page 4.
Formules approchées

Sélectionner l’affirmation exacte :
1- [A]. Exemple : pH < pka : la base reste prédominante
2- [B]. La relation n’est pas égale à : pH = ½ (pka + pKC)
3- Acides et bases faibles : des coefficients ½ apparaissent dans les relations
4- Pas la peine de vérifier, en fin de calculs, que les ions oxonium provenant de l’autoprotolyse de l’eau, sont en concentrations négligeables
L’affirmation 3 est exacte.
Affirmation 1
Non.
[A]. Exemple : pH < pka : l’acide reste prédominant.
Affirmation 2
Si.
[B]. La relation pH=1/2 (pKa-logC) peut aussi s’écrire :
pH = ½ (pka + pKC), puisque pKC = - log C
pKC, potentiel chimique de l’élément C introduit en concentration C.
Affirmation 4
Si.
En fin de
calculs, vérifier que le pH trouvé indique que les ions oxonium provenant de
l’autoprotolyse de l’eau sont en concentrations négligeables.
C’est le cas si :
- pour un acide, pH calculé est intérieur à 6,5
- pour une base, pH calculé est supérieur à 7,5
- Bases et acides forts. Conditions de validité des relations approchées.
[Concentration] >à 10-5 mol/L
(Les concentrations en acide fort ou en base forte ne doivent pas être trop faibles).
- Acides et bases faibles. Conditions de validité des relations approchées :
1 mol/L < [Concentration] < 10-6 mol/L
- Partant de la relation de base pH = pka + log ([Base] / [Acide]) on peut prouver la justesse des relations approchées utilisées pour les calculs.
(Faire une recherche Internet)
Page 5.
Calcul pH. Acide fort

Sélectionner l’affirmation exacte :
1- [A]. pH = 2 : L’acide chlorhydrique est un acide faible
2- [B]. Log [1]=0, Log [0,1]=-2, Log [0,01]=-3, Log [10^7]=7
3- Le logarithme décimal des nombres inférieurs à 1 sont positifs
4- Les coefficients stoechiométriques n’entrent pas dans le calcul pH=-log [concentration]
L’affirmation 2 est exacte.
Affirmation 1
Non.
Ne pas confondre le pH et le pKa.
Le pKa de l’acide chlorhydrique = -3 (voir tables de pKa) : acide fort.
(Acides forts, pka < -2)
Le pH est le -log de la concentration d’H3O+ dans la solution.
Le pH dépend de la concentration, de la température, et caractérise l’état plus ou moins acide de la solution.
Affirmation 2
Oui.
[B].
Log [1]=0,
Log [0,1]=-2, Log [0,01]=-3, Log [10^7]= 7
Le logarithme décimal est le nombre de fois dont un nombre doit être multiplié pour obtenir le nombre voulu. C’est un exposant.
Exemple :
10 000 000 = 10^7 = 10 puissance 7 = 10x10x10x10x10x10x10
Log10 10 000 000 = 7
Il faut multiplier sept fois pour obtenir 10 000 000.
Affirmation 3
Non.
Les logarithmes décimaux des nombres inférieurs à 1 sont négatifs.
Affirmation 4
Si.
Les coefficients stoechiométriques entrent dans le calcul
pH=-log [coeff x concentration]
Exemple :
H2SO4 -> 2 H+ + SO4-
0,1 mole d’acide donne 2 x 0,1 moles de protons et 0,1 mole de base associée.
pH = - log [2 x 0,1]
(Multiplier la concentration par son coefficient stoechiométrique)
Acide fort : complètement dissocié en proton H+ et en base associée.
Sont considérés acides forts les acides à partir de pka = -2
[H+] = [AH] initiale
[AH] finale = 0
pH = - log [H+]
Page 6.
Calcul pH. Base forte

Sélectionner les deux affirmations exactes :
1- [Base forte initiale] = Concentration finale ions H3O+
2- KOH = base, donc : KOH + H => KOH2
3- La soude, hydroxyde de sodium NaOH, ou la potasse, hydroxyde de potassium KOH sont des exemples de bases fortes
4- [A]. pH = - log 0,25 = 0,6
5- [B]. Attention, KOH est un complexe. Il se dissocie directement en ions K et ions HO-, sans former d’acide conjugué
6- [B]. Si l’on dilue 10 fois la solution, le pH sera divisé par 10
Les affirmations 3 et 5 sont exactes.
Affirmation 1
Non.
[OH-] = [Base]0
Concentration finale ions hydroxyles HO- = [Base forte initiale]
Une base forte se dissocie presque complètement HO- et en acide conjugué BH.
Affirmation 2
Non.
KOH est une base mais aussi un « complexe ».
Les complexes se dissocient dans l’eau, « Réaction de complexation ».
KOH + H2O => K+ + H2O + OH-
Affirmation 4
Non.
[A].
La dissociation d’une [base] donne des ions hydroxyles [HO-].
Le pH est le –log [H3O+].
il faut trouver la concentration des ions oxonium à partir de la concentration
des hydroxyles.
Ke= [HO-].[H3O+]=14^-14
Et pOH=- log[HO-]
Dans le cas d’une base, pH = Ke – pOH = 14 – log 0,25 = 14 - 0,6 = 13,4
Affirmation 6
Non.
[B]. Si l’on dilue 10 fois la solution, refaire les calculs, comme présents réponse 4, en prenant la concentration divisée par 10 : 0,5 10-2 mol/L.
Page 7.
Calcul pH. Acide faible

Sélectionner l’affirmation exacte :
1- Formule approchée pour le calcul du pH d’un acide faible : pH= pka+logC
2- [A]. pH = 1,5
3- [A]. On peut utiliser la formule des acides faibles pour 2 raisons : on nous dit que pka = 4 (= acide faible) et le pH trouvé est plus petit que 4-1
4- [B]. L’acide AH s’est entièrement dissocié
L’affirmation 3 est exacte.
Affirmation 1
Non.
pH = ½ (pKa – logC0)
pKC0= -logC0
pH = ½ (pKa + pkC0)
C0 : concentration initiale d’acide.
Formules à savoir par coeur.
Affirmation 4
Non.
[B]. Seulement 62% des moles initiales d’acide se sont dissociées : l’acide est un acide faible.
Concentration oxonium à partir du pH :
[H3O+]= 10^-3,2 = 0,0062 mol.L-1
Calcul du pka à partir du pH et de la concentration initiale:
3,2 = 1/2pka -1/2 logC0 = ½ pka - ½Log 0,01 = ½ pka +1
pka= 4,4
Page 8.
Calcul pH. Base faible

Sélectionner l’affirmation exacte :
1- Acides et bases : même formule de calculs approchés du pH
2- [A]. Base : espèce chimique qui en solution donne des ions hydroxydes HO-
3- pKa = 9,2 : base forte
L’affirmation 2 est exacte.
Affirmation 1
Non.
Acide faible : pH = ½ (pka + pkC)
Base faible : pH = ½ (pke + pka – pkc)
Affirmation 2
Oui.
Base : espèce chimique qui en solution donne des ions hydroxydes HO-
Les ions HO- peuvent provenir :
- de la dissociation de la base : BOH -> B+ + HO-
- de la décomposition de H2O : A- + H2O -> AH + HO-
Affirmation 3
Non.
pKa = 9,2 : base faible.
Bases fortes : pKa = 14 et plus.
Exemples de bases fortes : Oxyde de sodium-hydroxyde de sodium (Na2O, NaOH), oxyde de potassium-hydroxyde de potassium (K2O,KOH), oxyde de calcium-hydroxyde de calcium (CaO, Ca(OH)2), O2-, ...